题目内容
3.计算:(1($\sqrt{5}$-2)($\sqrt{5}$+2)
(2)$\sqrt{2}$-$\sqrt{\frac{1}{2}}$+3$\sqrt{8}$
(3)$\sqrt{12}$($\sqrt{75}$+3$\sqrt{\frac{1}{3}}$-$\sqrt{48}$)
(4)$\sqrt{48}$÷$\sqrt{3}$-$\sqrt{\frac{1}{2}}$×$\sqrt{12}$+$\sqrt{24}$.
分析 (1)直接利用平方差公式计算得出答案;
(2)首先化简二次根式进而得出答案;
(3)首先化简二次根式进而得出答案;
(4)直接利用二次根式乘除运算法则化简求出答案.
解答 解:(1)($\sqrt{5}$-2)($\sqrt{5}$+2)=5-4=1;
(2)$\sqrt{2}$-$\sqrt{\frac{1}{2}}$+3$\sqrt{8}$=$\sqrt{2}$-$\frac{\sqrt{2}}{2}$+6$\sqrt{2}$=$\frac{13\sqrt{2}}{2}$;
(3)$\sqrt{12}$($\sqrt{75}$+3$\sqrt{\frac{1}{3}}$-$\sqrt{48}$)
=2$\sqrt{3}$(5$\sqrt{3}$+$\sqrt{3}$-4$\sqrt{3}$)
=2$\sqrt{3}$×2$\sqrt{3}$
=12;
(4)$\sqrt{48}$÷$\sqrt{3}$-$\sqrt{\frac{1}{2}}$×$\sqrt{12}$+$\sqrt{24}$
=4-$\sqrt{6}$+2$\sqrt{6}$
=4+$\sqrt{6}$.
点评 此题主要考查了二次根式的混合运算,正确化简二次根式是解题关键.

练习册系列答案
相关题目
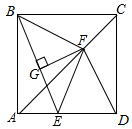 如图,在正方形ABCD中,点E是边AD上任意一点,BE的垂直平分线FG交对角AC于点F.求证:
如图,在正方形ABCD中,点E是边AD上任意一点,BE的垂直平分线FG交对角AC于点F.求证:
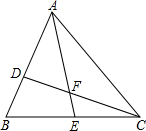 如图,点D在△ABC边AB上且AD:BD=2:1,E是BC的中点,设S1为△ADF的面积,S2为△CEF的面积.若S△ABC=24,则S1-S2=4.
如图,点D在△ABC边AB上且AD:BD=2:1,E是BC的中点,设S1为△ADF的面积,S2为△CEF的面积.若S△ABC=24,则S1-S2=4.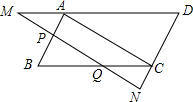 已知:?ABCD中,直线MN∥AC,分别交DA延长线于M,DC延长线于N,AB于P,BC于Q.求证:PM=QN.
已知:?ABCD中,直线MN∥AC,分别交DA延长线于M,DC延长线于N,AB于P,BC于Q.求证:PM=QN.