题目内容
已知关于x的一元二次方程2x2+x+m=0.
(1)当m=1时,判断方程的根的情况;
(2)当m=-1时,求方程的根.
(1)当m=1时,判断方程的根的情况;
(2)当m=-1时,求方程的根.
考点:根的判别式,解一元二次方程-因式分解法
专题:
分析:(1)把m=1代入△=b2-4ac,再判断出△的符号即可;
(2)把m=-1代入△=b2-4ac,得出△>0,再根据一元二次方程的求根公式进行计算即可.
(2)把m=-1代入△=b2-4ac,得出△>0,再根据一元二次方程的求根公式进行计算即可.
解答:解:(1)当m=1时,△=1-4×2×1=-7<0,
则原方程无解;
(2)当m=-1时,
∵△=1-4×2×(-1)=9>0,
∴x=
=
,
∴x1=
,x2=-1.
则原方程无解;
(2)当m=-1时,
∵△=1-4×2×(-1)=9>0,
∴x=
-1±
| ||
| 4 |
| -1±3 |
| 4 |
∴x1=
| 1 |
| 2 |
点评:此题考查了根的判别式和一元二次方程的解法,一元二次方程根的情况与判别式△的关系:(1)△>0?方程有两个不相等的实数根;(2)△=0?方程有两个相等的实数根;(3)△<0?方程没有实数根.

练习册系列答案
相关题目
下列计算正确的是( )
| A、2x+3y=5xy |
| B、x4•x4=x16 |
| C、(4x8)÷(2x2)=2x6 |
| D、(a3)2•a4=a9 |
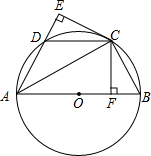 已知:如图,AB是⊙O的直径,点C、D为圆上两点,且CB=CD,CF⊥AB于点F,CE⊥AD的延长线于点E.
已知:如图,AB是⊙O的直径,点C、D为圆上两点,且CB=CD,CF⊥AB于点F,CE⊥AD的延长线于点E. 长方体的主视图、俯视图如图,则其左视图面积为
长方体的主视图、俯视图如图,则其左视图面积为