题目内容
17.已知关于a,b的方程组$\left\{\begin{array}{l}{a-b=2m+1}\\{a+b=4m+3}\end{array}\right.$.(1)若原方程组的解也是二元一次方程2a-3b=7的一个解,求m的值;
(2)若原方程组的解a,b满足a+2b<12,求不等式组$\left\{\begin{array}{l}{x-m<0}\\{4x+3>2x-1}\end{array}\right.$的解集.
分析 (1)解方程组得出a=3m+2、b=m+1,代入方程2a-3b=7,解之可得;
(2)将a、b代入a+2b<12得出m的范围,再解不等式组,根据解集的定义分类讨论可得.
解答 解:(1)解方程组得$\left\{\begin{array}{l}{a=3m+2}\\{b=m+1}\end{array}\right.$,
根据题意知2(3m+2)-3(m+1)=7,
解得:m=2;
(2)由题意知3m+2+2(m+1)<12,
解得:m<$\frac{8}{5}$,
解不等式x-m<0,得:x<m,
解不等式4x+3>2x-1,得:x>-2,
若m≤-2,则不等式组无解,
若-2$<m<\frac{8}{5}$,则不等式组的解集为-2<x<m.
点评 本题考查的是解二元一次方程组和解一元一次不等式组,正确求出每一个不等式解集是基础,根据题意得出关于m的方程或不等式是解答此题的关键.

练习册系列答案
相关题目
8.下列说法中正确的是( )
| A. | 最简分数的分子和分母都是素数 | |
| B. | 两个素数一定互素 | |
| C. | 数a的倒数是$\frac{1}{a}$ | |
| D. | 如果两个数互为倒数,那么它们的积一定是1 |
5.若m<0,mn<0,则|n-m+1|-|m-n-5|的值是( )
| A. | -4 | B. | 4 | C. | 2n-2m+4 | D. | 无法确定 |
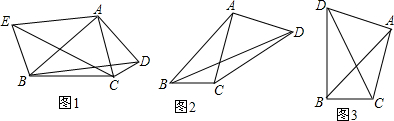
 如图,△ABC中,AB=AC,∠BAC=90°,在CB的延长线上取一点D,连接AD,过点A作AE⊥AD,过点C作CE⊥CB,AE与CE交于点E,连接BE,延长△ADC的中线AF交BE于点G.
如图,△ABC中,AB=AC,∠BAC=90°,在CB的延长线上取一点D,连接AD,过点A作AE⊥AD,过点C作CE⊥CB,AE与CE交于点E,连接BE,延长△ADC的中线AF交BE于点G.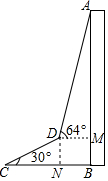 为了测量出大楼AB的高度,从距离楼底B处50米的点C(点C与楼底B在同一水平面上)出发,沿倾斜角为30°的斜坡CD前进20米到达点D,在点D处测得楼顶A的仰角为64°,求大楼AB的高度(结果精确到1米)(参考数据:sin64°≈0.9,cos64°≈0.4,tan64°≈2.1,$\sqrt{3}$≈1.7)
为了测量出大楼AB的高度,从距离楼底B处50米的点C(点C与楼底B在同一水平面上)出发,沿倾斜角为30°的斜坡CD前进20米到达点D,在点D处测得楼顶A的仰角为64°,求大楼AB的高度(结果精确到1米)(参考数据:sin64°≈0.9,cos64°≈0.4,tan64°≈2.1,$\sqrt{3}$≈1.7)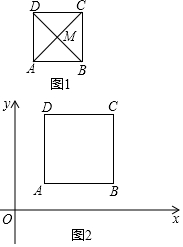 如果P是正方形ABCD内的一点,且满足∠APB+∠DPC=180°,那么称点P是正方形ABCD的对补点.
如果P是正方形ABCD内的一点,且满足∠APB+∠DPC=180°,那么称点P是正方形ABCD的对补点.