题目内容
13．计算（x4+1）（x2+1）（x+1）（x-1）的结果是（ ）| A． | x8+1 | B． | （x+1）8 | C． | x8-1 | D． | （x-1）8 |
分析 原式利用平方差公式计算即可得到结果．
解答 解：原式=（x4+1）（x2+1）（x2-1）=（x4+1）（x4-1）=x8-1，
故选C
点评 此题考查了平方差公式，熟练掌握平方差公式是解本题的关键．
练习册系列答案
相关题目
1．
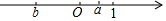已知实数a、b在数轴上的位置如图所示，则下列等式成立的是（ ）
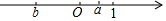已知实数a、b在数轴上的位置如图所示，则下列等式成立的是（ ）| A． | |a+b|=a+b | B． | |a+b|=a-b | C． | |a+1|=a+1 | D． | |b+1|=b+1 |
2．
在平面直角坐标系中，直线l：y=x-1与x轴交于点A1，如图所示依次作正方形A1B1C1O、正方形A2B2C2C1、…、正方形AnBnCnCn-1，使得点A1、A2、A3、…在直线l上，点C1、C2、C3、…在y轴正半轴上，则点Bn的横坐标是（ ）
在平面直角坐标系中，直线l：y=x-1与x轴交于点A1，如图所示依次作正方形A1B1C1O、正方形A2B2C2C1、…、正方形AnBnCnCn-1，使得点A1、A2、A3、…在直线l上，点C1、C2、C3、…在y轴正半轴上，则点Bn的横坐标是（ ）| A． | 2 | B． | 2n-1 | C． | 2n | D． | 2n+1 |
8．下列说法中正确的是（ ）
| A． | 最简分数的分子和分母都是素数 | |
| B． | 两个素数一定互素 | |
| C． | 数a的倒数是$\frac{1}{a}$ | |
| D． | 如果两个数互为倒数，那么它们的积一定是1 |
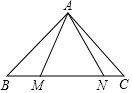如图，在等腰直角三角形ABC中，∠BAC=90°，AB=AC=15$\sqrt{2}$，点M、N在边BC上，且∠MAN=45°，CN=5，MN=13．
5．若m＜0，mn＜0，则|n-m+1|-|m-n-5|的值是（ ）
| A． | -4 | B． | 4 | C． | 2n-2m+4 | D． | 无法确定 |
如图，△ABC中，AB=AC，∠BAC=90°，在CB的延长线上取一点D，连接AD，过点A作AE⊥AD，过点C作CE⊥CB，AE与CE交于点E，连接BE，延长△ADC的中线AF交BE于点G．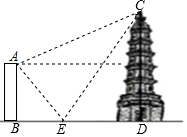
如图．大楼AB高16米，远处有一塔CD，某人在楼与塔间的平地E处测得塔顶的仰角为60°，楼顶的仰角为45°，爬到楼顶A处测得塔顶的仰角为30°，求塔CD的高度及大楼与塔之间的距离BD的长度．（结果精确到0.1米，参考数据：$\sqrt{2}≈$1.41，$\sqrt{3}≈$1.73）