题目内容
为方便市民出行,减轻城市中心烦交通压力,西安市修建了贯穿东西、南北的地铁1、2号线,已知修建地铁1号线24千米和2号线26千米共投资245.2亿元;且2号线每千米的平均造价比1号线每千米的平均造价多0.2亿元.
(1)求1号线,2号线每千米的平均造价分别是多少亿元?
(2)除1,2号线外,西安市政府规划还要再建201千米的地铁线网.据预算,这201千米地铁线网每千米的平均造价是2号线每千米的平均造价的1.2倍,则还需投资多少亿元?
(1)求1号线,2号线每千米的平均造价分别是多少亿元?
(2)除1,2号线外,西安市政府规划还要再建201千米的地铁线网.据预算,这201千米地铁线网每千米的平均造价是2号线每千米的平均造价的1.2倍,则还需投资多少亿元?
考点:二元一次方程组的应用
专题:
分析:(1)设1号线,2号线每千米的平均造价分别是x亿元、y亿元,根据修建地铁1号线24千米和2号线26千米共投资245.2亿元,2号线每千米的平均造价比1号线每千米的平均造价多0.2亿元,列方程组求解;
(2)求出每千米的造价,然后求出总投资.
(2)求出每千米的造价,然后求出总投资.
解答:解:(1)设1号线,2号线每千米的平均造价分别是x亿元、y亿元,
由题意得,
,
解得:
.
答:1号线,2号线每千米的平均造价分别是4.8亿元,5亿元;
(2)每千米的总造价为:5×1.2=6(元),
201×6=1206(亿元).
答:还需投资1206亿元.
由题意得,
|
解得:
|
答:1号线,2号线每千米的平均造价分别是4.8亿元,5亿元;
(2)每千米的总造价为:5×1.2=6(元),
201×6=1206(亿元).
答:还需投资1206亿元.
点评:本题考查了二元一次方程组的应用,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程组求解.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
下列各组数,互为相反数的一组是( )
| A、-23与(-2)3 |
| B、32与-23 |
| C、(-3)2与-32 |
| D、(-3×2)2与-3×23 |
已知关于x的方程2x2-3kx+k=0的一个根为1,则它的另一个根及k的值分别为( )
A、
| ||
B、1,
| ||
C、2,
| ||
D、
|
下列各式中,正确的是( )
| A、4a-(b+c)=4a-b+c |
| B、4a-(b+c)=4a+b-c |
| C、4a-(b+c)=4a+b+c |
| D、4a-(b+c)=4a-b-c |
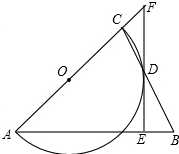 如图,△ABC是等腰三角形,AB=AC,以AC为直径的⊙O与BC交于点D,DE⊥AB,垂足为E,ED的延长线与AC的延长线交于点F.
如图,△ABC是等腰三角形,AB=AC,以AC为直径的⊙O与BC交于点D,DE⊥AB,垂足为E,ED的延长线与AC的延长线交于点F.