题目内容
2.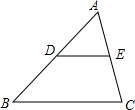 如图,△ABC中,点DE分别是ABAC的中点,则下列结论:
如图,△ABC中,点DE分别是ABAC的中点,则下列结论:①BC=2DE;②△ADE∽△ABC;③$\frac{AD}{AE}=\frac{AB}{AC}$.
其中正确的有3个.
分析 由已知条件得出DE是△ABC的中位线,由三角形中位线定理得出DE∥BC,DE=$\frac{1}{2}$BC,得出BC=2DE,△ADE∽△ABC,得出$\frac{AD}{AE}=\frac{AB}{AC}$,得出①②③正确,即可得出结论.
解答 解:∵点D、E分别是AB、AC的中点,
∴DE是△ABC的中位线,
∴DE∥BC,DE=$\frac{1}{2}$BC,
∴BC=2DE,△ADE∽△ABC,
∴$\frac{AD}{AE}=\frac{AB}{AC}$,
∴①②③正确,
正确的有3个,故答案为:3.
点评 本题考查了三角形中位线定理、相似三角形的判定与性质;熟练掌握三角形中位线定理,并能进行推理论证是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.下列说法中正确的是( )
| A. | 画一条3厘米长的直线 | B. | 画一条3厘米长的射线 | ||
| C. | 画一条3厘米长的线段 | D. | 在直线、射线、线段中直线最长 |
17.中华人民共和国国家统计局2003年2月28日统计:综 合国民经济持续较快增长.全年国内生产总值跃上10万亿元的新台阶,达到102398亿元,按可比价格计算,比上年增长8%.(见图)把102 398用科学记数法表示为( )亿元.


| A. | 1.02398×105 | B. | 10.2398×104 | C. | 1.02398×106 | D. | 0.102398×107 |
 如图,线段AB的两个端点坐标分别为A(1,1),B(2,1),以原点O为位似中心,将线段AB放大后得到线段CD,若CD=2,则端点C的坐标为(2,2).
如图,线段AB的两个端点坐标分别为A(1,1),B(2,1),以原点O为位似中心,将线段AB放大后得到线段CD,若CD=2,则端点C的坐标为(2,2). 如图,在△ABC中,E,F是边BC上的两个三等分点,D是AC的中点,BD分别交AE,AF,AC于P,Q,D,求BP:PQ:QD.
如图,在△ABC中,E,F是边BC上的两个三等分点,D是AC的中点,BD分别交AE,AF,AC于P,Q,D,求BP:PQ:QD. 如图,已知DA∥FE∥CB,且DA=CB,求证:$\frac{EA}{AM}$=$\frac{EB}{BN}$.
如图,已知DA∥FE∥CB,且DA=CB,求证:$\frac{EA}{AM}$=$\frac{EB}{BN}$.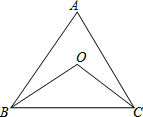 如图,点0是△ABC的∠ABC、∠ACB的平分线的交点,
如图,点0是△ABC的∠ABC、∠ACB的平分线的交点,