题目内容
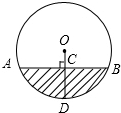 如图,水平放置的一个油管的截面半径为12cm,其中有油部分油面宽AB为12
如图,水平放置的一个油管的截面半径为12cm,其中有油部分油面宽AB为12| 3 |
考点:垂径定理的应用,勾股定理,扇形面积的计算
专题:
分析:连接OA、OB,由于油面宽AB为12
cm可求出AC的长,在Rt△AOC中利用三角函数的定义可求出∠AOC的度数,由垂径定理可知,∠AOC=∠BOC,进而可求出∠AOB的度数,根据扇形及三角形的面积可求出弓形的面积.
| 3 |
解答: 解:连接OA、OB,
解:连接OA、OB,
∵AB=12
cm,
∴AC=6
cm,
∵OA=OD=12cm,
∴sin∠AOC=
=
=
,
∴∠AOC=60°
∴AC=OA•cos∠AOC=12×
=6cm,∠AOB=2∠AOE=2×60°=120°,
∴S阴影=S扇形OAB-S△OAB=
-
×12
×6=48π-36
cm2.
故答案为:(48π-36
).
 解:连接OA、OB,
解:连接OA、OB,∵AB=12
| 3 |
∴AC=6
| 3 |
∵OA=OD=12cm,
∴sin∠AOC=
| AC |
| OA |
6
| ||
| 12 |
| ||
| 2 |
∴∠AOC=60°
∴AC=OA•cos∠AOC=12×
| 1 |
| 2 |
∴S阴影=S扇形OAB-S△OAB=
| 120×π×122 |
| 360 |
| 1 |
| 2 |
| 3 |
| 3 |
故答案为:(48π-36
| 3 |
点评:本题考查的是垂径定理的应用及勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
下列合并同类项中结果正确的是( )
| A、5a+2b=7ab |
| B、4x2-2x2=2 |
| C、-2ab2+2b2a=0 |
| D、x2+x2=2x4 |
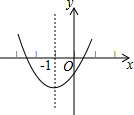 已知二次函数y=ax2+bx+c的图象如图所示,其对称轴为直线x=-1,给出下列结论:(1)b2>4ac;(2)abc>0;(3)2a+b=0;(4)a+b+c>0;(5)4a-2b+c<0.则正确的结论有( )
已知二次函数y=ax2+bx+c的图象如图所示,其对称轴为直线x=-1,给出下列结论:(1)b2>4ac;(2)abc>0;(3)2a+b=0;(4)a+b+c>0;(5)4a-2b+c<0.则正确的结论有( )| A、2个 | B、3个 | C、4个 | D、5个 |
 如图是一个正方体的展开图,则和“希”字相对的是( )
如图是一个正方体的展开图,则和“希”字相对的是( )| A、你 | B、能 | C、成 | D、功 |
 如图,在Rt△ABC,∠C=90°,AC=8,BC=6,则sinB的值等于( )
如图,在Rt△ABC,∠C=90°,AC=8,BC=6,则sinB的值等于( )A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,AB=AC,则数轴上点C所表示的数为( )
如图,AB=AC,则数轴上点C所表示的数为( )A、
| ||
B、-
| ||
C、-
| ||
D、
|
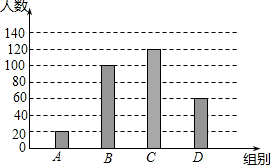 国家规定,中、小学生每天在校体育活动时间不低于1h,为此,某市就“你每天在校体育活动时间是多少”的问题随机调查了辖区内300名初中学生.根据调查结果绘制的统计图如图所示,其中分组情况是A组:t<0.5h;B组:0.5h<0<1h;C组:1h<t<1.5h;D组:t≥1.5h.请根据上述信息解答下列问题:
国家规定,中、小学生每天在校体育活动时间不低于1h,为此,某市就“你每天在校体育活动时间是多少”的问题随机调查了辖区内300名初中学生.根据调查结果绘制的统计图如图所示,其中分组情况是A组:t<0.5h;B组:0.5h<0<1h;C组:1h<t<1.5h;D组:t≥1.5h.请根据上述信息解答下列问题: