题目内容
如图，在Rt△ABC，∠C=90°，AC=8，BC=6，则sinB的值等于（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
考点：锐角三角函数的定义
专题：
分析：先根据勾股定理求出AB的长，再运用锐角三角函数的定义解答．
解答：解：∵Rt△ABC中，∠C=90°，AC=8，BC=6，
∴AB=
=10，
∴sinB=
=
=
．
故选C．
∴AB=
| AC2+BC2 |
∴sinB=
| AC |
| AB |
| 8 |
| 10 |
| 4 |
| 5 |
故选C．
点评：本题考查了勾股定理和锐角三角函数的定义，比较简单．掌握正弦函数的定义是解题的关键．
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
某城中村改造项目约需人民币188000000元，那么188000000用科学记数法表示为（ ）
| A、1.88×108 |
| B、1.88×109 |
| C、1.9×108 |
| D、1.9×109 |
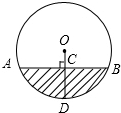如图，水平放置的一个油管的截面半径为12cm，其中有油部分油面宽AB为12
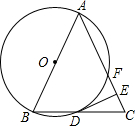如图，以等腰三角形ABC的腰AB为直径的⊙O交底边BC于点D，交腰AB于点F，过D点作DE⊥AC于E点，试确定直线DE与⊙O的位置关系，并说明理由．将抛物线y=2x2向右平移1个单位，再向上平移3个单位，得到的抛物线是（ ）
| A、y=2（x+1）2+3 |
| B、y=2（x-1）2+3 |
| C、y=2（x+1）2-3 |
| D、y=2（x-1）2-3 |
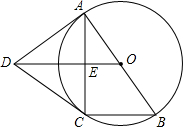如图，AB是⊙O直径，AC是弦，OE⊥AC于点E，过A作⊙O的切线DA，DA与OE的延长线交于点D，连接DC，BC．
如图，一次函数的图象与x轴、y轴分别相交于A、B两点，且与反比例函数的图象在第二象限交于点C．如果点A的坐标为（4，0），OA=2OB，点B是AC的中点．