题目内容
阅读下面材料:
小辉遇到这样一个问题:如图1,在Rt△ABC中,∠BAC=90°,AB=AC,点D,E在边BC上,∠DAE=45°.若BD=3,CE=1,求DE的长.
小辉发现,将△ABD绕点A按逆时针方向旋转90°,得到△ACF,连接EF(如图2),由图形旋转的性质和等腰直角三角形的性质以及∠DAE=45°,可证△FAE≌△DAE,得FE=DE.解△FCE,可求得FE(即DE)的长.
请回答:在图2中,∠FCE的度数是 ,DE的长为 .
参考小辉思考问题的方法,解决问题:
如图3,在四边形ABCD中,AB=AD,∠B+∠D=180°.E,F分别是边BC,CD上的点,且∠EAF=
∠BAD.猜想线段BE,EF,FD之间的数量关系并说明理由.
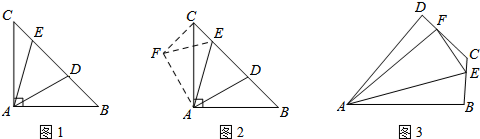
小辉遇到这样一个问题:如图1,在Rt△ABC中,∠BAC=90°,AB=AC,点D,E在边BC上,∠DAE=45°.若BD=3,CE=1,求DE的长.
小辉发现,将△ABD绕点A按逆时针方向旋转90°,得到△ACF,连接EF(如图2),由图形旋转的性质和等腰直角三角形的性质以及∠DAE=45°,可证△FAE≌△DAE,得FE=DE.解△FCE,可求得FE(即DE)的长.
请回答:在图2中,∠FCE的度数是
参考小辉思考问题的方法,解决问题:
如图3,在四边形ABCD中,AB=AD,∠B+∠D=180°.E,F分别是边BC,CD上的点,且∠EAF=
| 1 |
| 2 |

考点:旋转的性质,全等三角形的判定与性质
专题:探究型
分析:对于图2,由旋转性质得到∠ACF=∠B=45°,CF=BD,所以∠FCE=∠ACF+∠ACB=90°,然后利用勾股定理计算EF,即可得到DE;
对于图3,将△ABE绕点A按逆时针方向旋转,使AB与AD重合,得到△ADG,根据旋转的性质得BE=DG,AE=AG,∠DAG=∠BAE,∠B=∠ADG,由于∠B+∠ADC=180°,则∠ADG+∠ADC=180°,则可判断点F,D,G在同一条直线上,接着证明△AEF≌△AGF,得到EF=FG,由于FG=DG+FD=BE+DF,于是得到EF=BE+FD.
对于图3,将△ABE绕点A按逆时针方向旋转,使AB与AD重合,得到△ADG,根据旋转的性质得BE=DG,AE=AG,∠DAG=∠BAE,∠B=∠ADG,由于∠B+∠ADC=180°,则∠ADG+∠ADC=180°,则可判断点F,D,G在同一条直线上,接着证明△AEF≌△AGF,得到EF=FG,由于FG=DG+FD=BE+DF,于是得到EF=BE+FD.
解答: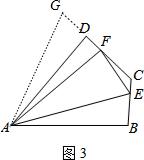 解:如图2,∵∠ACF=∠B=45°,
解:如图2,∵∠ACF=∠B=45°,
∴∠FCE=∠ACF+∠ACB=45°+45°=90°,
在Rt△EFC中,∵CF=BD=3,CE=1,
∴EF=
=
=
,
∴DE=
,
故答案为90°;
;
如图3,
猜想:EF=BE+FD.理由如下:
如图,将△ABE绕点A按逆时针方向旋转,使AB与AD重合,得到△ADG,
∴BE=DG,AE=AG,∠DAG=∠BAE,∠B=∠ADG,
∵∠B+∠ADC=180°,
∴∠ADG+∠ADC=180°,即点F,D,G在同一条直线上,
∵∠DAG=∠BAE,
∴∠GAE=∠BAD,
∵∠EAF=
∠BAD,
∴∠GAF=∠EAF,
在△AEF和△AGF中,
,
∴△AEF≌△AGF(SAS),
∴EF=FG,
∵FG=DG+FD=BE+DF,
∴EF=BE+FD.
 解:如图2,∵∠ACF=∠B=45°,
解:如图2,∵∠ACF=∠B=45°,∴∠FCE=∠ACF+∠ACB=45°+45°=90°,
在Rt△EFC中,∵CF=BD=3,CE=1,
∴EF=
| CF2+CE2 |
| 32+12 |
| 10 |
∴DE=
| 10 |
故答案为90°;
| 10 |
如图3,
猜想:EF=BE+FD.理由如下:
如图,将△ABE绕点A按逆时针方向旋转,使AB与AD重合,得到△ADG,
∴BE=DG,AE=AG,∠DAG=∠BAE,∠B=∠ADG,
∵∠B+∠ADC=180°,
∴∠ADG+∠ADC=180°,即点F,D,G在同一条直线上,
∵∠DAG=∠BAE,
∴∠GAE=∠BAD,
∵∠EAF=
| 1 |
| 2 |
∴∠GAF=∠EAF,
在△AEF和△AGF中,
|
∴△AEF≌△AGF(SAS),
∴EF=FG,
∵FG=DG+FD=BE+DF,
∴EF=BE+FD.
点评:本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了全等三角形的判定与性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
某城中村改造项目约需人民币188000000元,那么188000000用科学记数法表示为( )
| A、1.88×108 |
| B、1.88×109 |
| C、1.9×108 |
| D、1.9×109 |
 已知线段a、c,求作直角△ABC,使∠C=90°,BC=a,AB=c.
已知线段a、c,求作直角△ABC,使∠C=90°,BC=a,AB=c.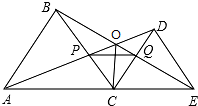 已知,如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作等边三角形ABC和等边三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ,OC,以下四个结论:
已知,如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作等边三角形ABC和等边三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ,OC,以下四个结论: 如图,水平放置的一个油管的截面半径为12cm,其中有油部分油面宽AB为12
如图,水平放置的一个油管的截面半径为12cm,其中有油部分油面宽AB为12