题目内容
已知a是不为1的有理数,我们把
称为a的差倒数,如:2的差倒数是
=-1.
现已知a1=
,a2是a1的差倒数,a3是a2的差倒数,a4是a3的差倒数,
(1)求a2,a3,a4的值;
(2)根据(1)的计算结果,请猜想并写出a2012•a2013•a2014的值;
(3)计算:a1+a2+a3+a2012+a2013.
| 1 |
| 1-a |
| 1 |
| 1-2 |
现已知a1=
| 1 |
| 2 |
(1)求a2,a3,a4的值;
(2)根据(1)的计算结果,请猜想并写出a2012•a2013•a2014的值;
(3)计算:a1+a2+a3+a2012+a2013.
考点:规律型:数字的变化类,倒数
专题:新定义,规律型
分析:(1)由题意得:a2=
=2,a3=
=-1,a4=
=
;
(2)从(1)的计算结果可以看出,从a1开始,每三个数一循环,而2012÷3=670余2,则a2012=a2=2,a2013=a3=-1,a2014=a1=
,然后计算a2012•a2013•a2014的值;
(3)由于a1•a2•a3=a4•a5•a6=…a2008•a2009•a2010=a2011•a2012•a2013=-1,把a1•a2•a3…a2010•a2011•a2012•a2013分成(a1•a2•a3)•(a4•a5•a6)…(a2008•a2009•a2010)•(a2011•a2012•a2013),然后代值计算即可.
| 1 | ||
1-
|
| 1 |
| 1-2 |
| 1 |
| 1-(-1) |
| 1 |
| 2 |
(2)从(1)的计算结果可以看出,从a1开始,每三个数一循环,而2012÷3=670余2,则a2012=a2=2,a2013=a3=-1,a2014=a1=
| 1 |
| 2 |
(3)由于a1•a2•a3=a4•a5•a6=…a2008•a2009•a2010=a2011•a2012•a2013=-1,把a1•a2•a3…a2010•a2011•a2012•a2013分成(a1•a2•a3)•(a4•a5•a6)…(a2008•a2009•a2010)•(a2011•a2012•a2013),然后代值计算即可.
解答:解:(1)a1=
,a2=
=2,a3=
=-1,a4=
=
;
(2)∵2012÷3=670余2,∴a2012=a2=2,a2013=a3=-1,a2014=a1=
,∴a2012•a2013•a2014=2×(-1)×
=-1;
(3)∵a1+a2+a3=a4+a5+a6=…=a2008+a2009+a2010=a2011+a2012+a2013=
,
∴a1+a2+a3…a2010+a2011+a2012+a2013=(a1+a2+a3)+(a4+a5+a6)…(a2008+a2009+a2010)+(a2011+a2012+a2013)=
×671=1006
.
| 1 |
| 2 |
| 1 | ||
1-
|
| 1 |
| 1-2 |
| 1 |
| 1-(-1) |
| 1 |
| 2 |
(2)∵2012÷3=670余2,∴a2012=a2=2,a2013=a3=-1,a2014=a1=
| 1 |
| 2 |
| 1 |
| 2 |
(3)∵a1+a2+a3=a4+a5+a6=…=a2008+a2009+a2010=a2011+a2012+a2013=
| 3 |
| 2 |
∴a1+a2+a3…a2010+a2011+a2012+a2013=(a1+a2+a3)+(a4+a5+a6)…(a2008+a2009+a2010)+(a2011+a2012+a2013)=
| 3 |
| 2 |
| 1 |
| 2 |
点评:此类问题考查了数字类的变化规律,解决的关键是要严格根据定义进行解答,同时注意分析循环的规律.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
下列运算正确的是( )
| A、x+y=xy |
| B、5x3-2x3=3 |
| C、x2+3x3=4x5 |
| D、5x2y-4x2y=x2y |
下列事件属于必然事件的是( )
| A、随意翻到一本书的某页,这页的页码是奇数 |
| B、购买一张福利彩票,中奖 |
| C、在一个标准大气压下,水加热到100℃会沸腾 |
| D、抛一次骰子,向上一面的点数是7 |
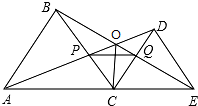 已知,如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作等边三角形ABC和等边三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ,OC,以下四个结论:
已知,如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作等边三角形ABC和等边三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ,OC,以下四个结论: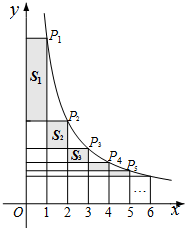 在函数
在函数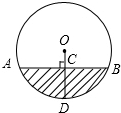 如图,水平放置的一个油管的截面半径为12cm,其中有油部分油面宽AB为12
如图,水平放置的一个油管的截面半径为12cm,其中有油部分油面宽AB为12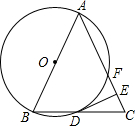 如图,以等腰三角形ABC的腰AB为直径的⊙O交底边BC于点D,交腰AB于点F,过D点作DE⊥AC于E点,试确定直线DE与⊙O的位置关系,并说明理由.
如图,以等腰三角形ABC的腰AB为直径的⊙O交底边BC于点D,交腰AB于点F,过D点作DE⊥AC于E点,试确定直线DE与⊙O的位置关系,并说明理由.