题目内容
9.将两块全等含有30°的直角三角板如图①摆放.
(1)将图①中的△A1B1C顺时针旋转45°得图②,点P1是A1C与AB的交点,点Q是A1B1与BC的交点,求证:CP1=CQ;
(2)在图②中,若AP1=2,则CQ等于多少?
(3)如图③,在B1C上取一点E,连接BE、P1E,设BC=1,当BE⊥P1B时,则△P1BE面积的最大值是$\frac{\sqrt{3}}{6}$.
分析 (1)先判断∠B1CQ=∠BCP1=45°,利用ASA即可证明△B1CQ≌△BCP1,从而得出结论.
(2)作P1D⊥CA于D,在RtADP1中,求出P1D,在Rt△CDP1中求出CP1,继而可得出CQ的长度.
(3)证明△AP1C∽△BEC,则有AP1:BE=AC:BC=$\sqrt{3}$:1,设AP1=x,则BE=$\frac{\sqrt{3}}{3}$x,得出S△P1BE关于x的表达式,利用配方法求最值即可.
解答 (1)证明:∵∠B1CB=45°,∠B1CA1=90°,
∴∠B1CQ=∠BCP1=45°,
∵在△B1CQ和△BCP1中,$\left\{\begin{array}{l}{∠{B}_{1}CQ=∠BC{P}_{1}}&{\;}\\{{B}_{1}C=BC}&{\;}\\{∠{B}_{1}=∠B}&{\;}\end{array}\right.$,
∴△B1CQ≌△BCP1(ASA),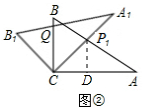
∴CQ=CP1;
(2)解:作P1D⊥CA于D,如图所示:
∵∠A=30°,
∴P1D=$\frac{1}{2}$AP1=1,
∵∠P1CD=45°,
∴$\frac{{P}_{1}D}{C{P}_{1}}$=sin45°=$\frac{\sqrt{2}}{2}$,
∴CP1=$\sqrt{2}$P1D=$\sqrt{2}$,
又∵CP1=CQ,
∴CQ=$\sqrt{2}$;
(3)解:∵∠P1BE=90°,∠ABC=60°,
∴∠A=∠CBE=30°,
∴AC=$\sqrt{3}$BC,
由旋转的性质可得:∠ACP1=∠BCE,
∴△AP1C∽△BEC,
∴AP1:BE=AC:BC=$\sqrt{3}$:1,
设AP1=x,则BE=$\frac{\sqrt{3}}{3}$x,
在Rt△ABC中,∠A=30°,
∴AB=2BC=2,
∴S△P1BE=$\frac{1}{2}$×$\frac{\sqrt{3}}{3}$x(2-x)=-$\frac{\sqrt{3}}{6}$x2+$\frac{\sqrt{3}}{3}$x
=-$\frac{\sqrt{3}}{6}$(x-1)2+$\frac{\sqrt{3}}{6}$,
故当x=1时,△P1BE面积的最大值是$\frac{\sqrt{3}}{6}$;
故答案为:$\frac{\sqrt{3}}{6}$.
点评 本题是三角形综合题目,考查了相似三角形的判定与性质、含30°角的直角三角形的性质、勾股定理及配方法求二次函数的最值;本题综合性强,有一定难度.

 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案| A. | 任何有理数的绝对值都是正数 | |
| B. | 任何有理数的绝对值都不可能小于0 | |
| C. | 1是最小的正数 | |
| D. | 最大的负数是-1 |
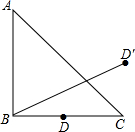 如图,在△ABC中,AB=BC,∠ABC=90°,D是BC的中点,且它关于AC的对称点是D′,BD′=$\sqrt{5}$,求AC的长.
如图,在△ABC中,AB=BC,∠ABC=90°,D是BC的中点,且它关于AC的对称点是D′,BD′=$\sqrt{5}$,求AC的长.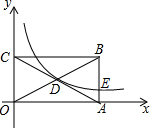 已知,矩形OABC中,BC=6,AB=4,它在平面直角坐标系中的位置如图所示,反比例函数y=$\frac{k}{x}$(k≠0)的图象经过矩形OABC对角线的交点D.
已知,矩形OABC中,BC=6,AB=4,它在平面直角坐标系中的位置如图所示,反比例函数y=$\frac{k}{x}$(k≠0)的图象经过矩形OABC对角线的交点D.