题目内容
20.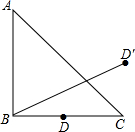 如图,在△ABC中,AB=BC,∠ABC=90°,D是BC的中点,且它关于AC的对称点是D′,BD′=$\sqrt{5}$,求AC的长.
如图,在△ABC中,AB=BC,∠ABC=90°,D是BC的中点,且它关于AC的对称点是D′,BD′=$\sqrt{5}$,求AC的长.
分析 连结CD′,DD′,由等腰直角三角形性质得∠ACB=45°,根据轴对称性质可得CD=CD′、∠D′CD=90°,由BC=2CD′可设CD′=x,则BC=2x,在Rt△BCD′中,由勾股定理即可得求得x的值,从而得出AB=BC=2,继而得出答案.
解答 解:如图,连结CD′,DD′,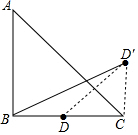
∵AB=BC,∠ABC=90°,
∴∠ACB=45°,
∵D关于AC的对称点是D′,
∴AC垂直平分DD′,
∴CD=CD′,∠D′CD=90°,
又∵D是BC的中点,
∴BC=2CD′,
设CD′=x,则BC=2x,
在Rt△BCD′中,由勾股定理得:CD′2+BC2=BD′2,即x2+(2x)2=5,
解得:x=1或x=-1(舍),
∴AB=BC=2,
∴AC=2$\sqrt{2}$.
点评 本题主要考查等腰直角三角形的性质、轴对称的性质及勾股定理,熟练掌握轴对称的性质是解题的关键.

练习册系列答案
相关题目
8.若|m-n|=n-m,且|m|=4,|n|=3,则(m+n)2=( )
| A. | 1 | B. | 36 | C. | 1或36 | D. | 1或49 |
10.下列画图语句中,正确的是( )
| A. | 画射线OP=3 cm | B. | 画出A、B两点的距离 | ||
| C. | 画出A、B两点的中点 | D. | 连结A、B两点 |
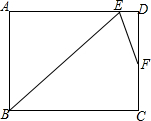 在矩形ABCD中,∠ABC的角平分线BE与AD交于点E,∠BED的角平分线EF与DC交于点F.若AB=9,F是CD的三等分点,则BC=6$\sqrt{2}$+3或3$\sqrt{2}$+6.
在矩形ABCD中,∠ABC的角平分线BE与AD交于点E,∠BED的角平分线EF与DC交于点F.若AB=9,F是CD的三等分点,则BC=6$\sqrt{2}$+3或3$\sqrt{2}$+6. 如图,在直角坐标系中,点A,点B的坐标分别为(2,0),(0,2)
如图,在直角坐标系中,点A,点B的坐标分别为(2,0),(0,2)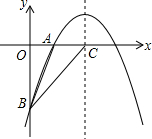 如图,已知二次函数y=-$\frac{1}{2}$x2+bx+c的图象经过A(2,0)、B(0,-6)两点.
如图,已知二次函数y=-$\frac{1}{2}$x2+bx+c的图象经过A(2,0)、B(0,-6)两点.