题目内容
19.观察下列各等式及验证过程.$\sqrt{\frac{1}{2}-\frac{1}{3}}$=$\frac{1}{2}$$\sqrt{\frac{2}{3}}$,验证$\sqrt{\frac{1}{2}-\frac{1}{3}}$=$\sqrt{\frac{1}{2×3}}$=$\sqrt{\frac{2}{{2}^{2}×3}}$=$\frac{1}{2}$$\sqrt{\frac{2}{3}}$;
$\sqrt{\frac{1}{2}(\frac{1}{3}-\frac{1}{4})}$=$\frac{1}{3}$$\sqrt{\frac{3}{8}}$,验证:$\sqrt{\frac{1}{2}(\frac{1}{3}-\frac{1}{4})}$=$\sqrt{\frac{1}{2×3×4}}$=$\sqrt{\frac{3}{2×{3}^{2}×4}}$=$\frac{1}{3}$$\sqrt{\frac{3}{8}}$;
$\sqrt{\frac{1}{3}(\frac{1}{4}-\frac{1}{5})}$=$\frac{1}{4}$$\sqrt{\frac{4}{15}}$,验证:$\sqrt{\frac{1}{3}(\frac{1}{4}-\frac{1}{5})}$=$\sqrt{\frac{1}{3×4×5}}$=$\sqrt{\frac{4}{3×{4}^{2}×5}}$=$\frac{1}{4}$$\sqrt{\frac{4}{15}}$.
(1)按照上述三个等式及其验证过程的基本思想,猜想$\sqrt{\frac{1}{4}(\frac{1}{5}-\frac{1}{6})}$的变形结果并进行验证.
(2)针对上述各式反映的规律,写出用n(n为正整数)表示的等式,并证明.
分析 (1)观察已知等式,将原式进行适当变形得到结果,验证即可;
(2)归纳总结得到一般性规律,写出结果,验证即可.
解答 解:(1)根据题意得:$\sqrt{\frac{1}{4}(\frac{1}{5}-\frac{1}{6})}$=$\frac{1}{5}$$\sqrt{\frac{5}{24}}$,
等式左边=$\sqrt{\frac{1}{4}×\frac{1}{30}}$=$\sqrt{\frac{1}{120}}$,右边=$\frac{1}{5}$$\sqrt{\frac{25}{120}}$=$\sqrt{\frac{1}{120}}$,
左边=右边,成立;
(2)归纳总结得:$\sqrt{\frac{1}{n+1}(\frac{1}{n+2}-\frac{1}{n+3})}$=$\frac{1}{n+2}$$\sqrt{\frac{n+2}{(n+1)(n+3)}}$(n为正整数),
证明:等式左边=$\sqrt{\frac{1}{(n+1)(n+2)(n+3)}}$,右边=$\frac{1}{n+2}$$\sqrt{\frac{(n+2)^{2}}{(n+1)(n+2)(n+3)}}$=$\sqrt{\frac{1}{(n+1)(n+2)(n+3)}}$,
左边=右边,成立.
点评 此题考查了实数的运算,弄清题中的规律是解本题的关键.

练习册系列答案
相关题目
10.下列画图语句中,正确的是( )
| A. | 画射线OP=3 cm | B. | 画出A、B两点的距离 | ||
| C. | 画出A、B两点的中点 | D. | 连结A、B两点 |
8. 如图,⊙O是△ABC的外接圆,已知∠B=60°,则∠CAO的度数是( )
如图,⊙O是△ABC的外接圆,已知∠B=60°,则∠CAO的度数是( )
 如图,⊙O是△ABC的外接圆,已知∠B=60°,则∠CAO的度数是( )
如图,⊙O是△ABC的外接圆,已知∠B=60°,则∠CAO的度数是( )| A. | 15° | B. | 30° | C. | 45° | D. | 60° |

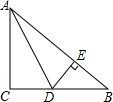 已知:如图,在△ABC中,∠C=90°,AC=BC,AD平分∠BAC交BC于点D,DE⊥AB于点E,若△DEB的周长为10cm,求斜边AB的长.
已知:如图,在△ABC中,∠C=90°,AC=BC,AD平分∠BAC交BC于点D,DE⊥AB于点E,若△DEB的周长为10cm,求斜边AB的长.