题目内容
4.山地自行车越来越受到中学生的喜爱,各种品牌相继投放市场,某车行经营的A型车去年销售总额为5万元,今年每辆销售价比去年降低400元,若卖出的数量相同,销售总额将比去年减少20%.(1)今年A型车每辆售价多少元?
(2)该车行计划新进一批A型车和新款B型车共60辆,要使这批车获利不少于33000元,A型车至多进多少辆?A,B两种型号车的进货和销售价格如表:
| A型车 | B型车 | |
| 进货价格(元) | 1100 | 1400 |
| 销售价格(元) | 今年的销售价格 | 2000 |
分析 (1)设今年A型车每辆售价x元,则去年售价每辆为(x+400)元,由卖出的数量相同建立方程求出其解即可;
(2)设今年新进A型车a辆,则B型车(60-a)辆,获利不少于33000元,由条件表示出33000与a之间的关系式,进而得出答案.
解答 解:(1)设今年A型车每辆售价x元,则去年售价每辆为(x+400)元,由题意,得:
$\frac{50000}{x+400}$=$\frac{50000(1-20%)}{x}$,
解得:x=1600.
经检验,x=1600是原方程的根.
答:今年A型车每辆售价1600元;
(2)设今年新进A型车a辆,则B型车(60-a)辆,由题意,得
(1600-1100)a+(2000-1400)(60-a)≥33000,
解得:a≤30,
故要使这批车获利不少于33000元,A型车至多进30辆.
点评 本题考查了列分式方程解实际问题的运用以及一元一次不等式的应用,得出正确不等关系是解题关键.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
15.四边形ABCD的对角线互相平分,要使它变为矩形,需要添加的条件是( )
| A. | AB=CD | B. | AC=BD | C. | AB=BC | D. | AD=BC |
19. 如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处,若∠A=25°,则∠BDC等于( )
如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处,若∠A=25°,则∠BDC等于( )
 如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处,若∠A=25°,则∠BDC等于( )
如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处,若∠A=25°,则∠BDC等于( )| A. | 44° | B. | 60° | C. | 67° | D. | 70° |
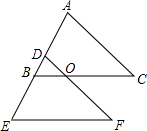 如图所示,△ABC平移后得到△DEF.
如图所示,△ABC平移后得到△DEF. 已知:如图,BD平分∠ABC,BE分∠ABC为2:5两部分,∠DBE=24°,求∠ABE的度数.
已知:如图,BD平分∠ABC,BE分∠ABC为2:5两部分,∠DBE=24°,求∠ABE的度数.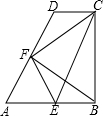 如图,在直角梯形ABCD中,AB∥DC,AB⊥BC,∠A=60°,AB=2CD,E、F分别为AB、AD的中点,连接EF、EC、BF、CF.则①四边形AECD为平行四边形;②△AEF为等边三角形;③△FDC与△BEF为全等的等腰三角形;④△AFB≌△EFC,其中正确的结论有①②③④(写出正确的序号即可)
如图,在直角梯形ABCD中,AB∥DC,AB⊥BC,∠A=60°,AB=2CD,E、F分别为AB、AD的中点,连接EF、EC、BF、CF.则①四边形AECD为平行四边形;②△AEF为等边三角形;③△FDC与△BEF为全等的等腰三角形;④△AFB≌△EFC,其中正确的结论有①②③④(写出正确的序号即可)