题目内容
17.有一列数如下排列-$\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{3}}{4}$,$\frac{1}{4}$,-$\frac{\sqrt{5}}{16}$,-$\frac{\sqrt{6}}{32}$,$\frac{\sqrt{7}}{64}$…,则第2015个数是( )| A. | $\frac{\sqrt{2015}}{{2}^{2015}}$ | B. | -$\frac{\sqrt{2015}}{{2}^{2015}}$ | C. | $\frac{\sqrt{2016}}{{2}^{2015}}$ | D. | -$\frac{\sqrt{2016}}{{2}^{2015}}$ |
分析 观察所给数字可知:第一个数字是-$\frac{\sqrt{2}}{2}$=-$\frac{\sqrt{2}}{{2}^{1}}$;第二个数字是-$\frac{\sqrt{3}}{4}$=-$\frac{\sqrt{3}}{{2}^{2}}$;第三个数字是$\frac{1}{4}$=$\frac{\sqrt{4}}{{2}^{3}}$;第四个数字是-$\frac{\sqrt{5}}{16}$=-$\frac{\sqrt{5}}{{2}^{4}}$;继而即可总结规律,求出第2015个数.
解答 解:观察可以发现:第一个数字是-$\frac{\sqrt{2}}{2}$=-$\frac{\sqrt{2}}{{2}^{1}}$;
第二个数字是-$\frac{\sqrt{3}}{4}$=-$\frac{\sqrt{3}}{{2}^{2}}$;
第三个数字是$\frac{1}{4}$=$\frac{2}{8}$=$\frac{\sqrt{4}}{{2}^{3}}$;
第四个数字是-$\frac{\sqrt{5}}{16}$=-$\frac{\sqrt{5}}{{2}^{4}}$;
…;
可得第2015个数即是-$\frac{\sqrt{2016}}{{2}^{2015}}$,
故选D.
点评 本题主要考查了数字变化,算式平方根的性质,数列规律问题,找出一般规律是解题的关键.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
7.据统计,我国今年夏粮的播种面积大约为415000000亩,415000000用科学记数法表示为( )
| A. | 4.15×107 | B. | 4.15×108 | C. | 41.5×107 | D. | 41.5×108 |
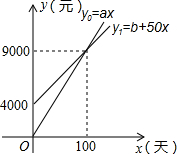 国家推行“节能减排,低碳经济“的政策后,某企业推出一种叫“CNG”的改烧汽油为天然气的装置,每辆车改装费为b元,据市场调查知:每辆车改装前、后的燃料费(含改装费)y0、y1(单位:元)与正常运营时间(单位:天)之间分别满足关系式:y0=ax,y1=b+50x,如图所示,试根据图象解决下列问题:
国家推行“节能减排,低碳经济“的政策后,某企业推出一种叫“CNG”的改烧汽油为天然气的装置,每辆车改装费为b元,据市场调查知:每辆车改装前、后的燃料费(含改装费)y0、y1(单位:元)与正常运营时间(单位:天)之间分别满足关系式:y0=ax,y1=b+50x,如图所示,试根据图象解决下列问题: