题目内容
如图，A、B、C为⊙O上三点，且 |
| AB |
|
| BC |
|
| CA |
（1）试确定△ABC的形状；
（2）若AB=a，求⊙O的半径．
考点：圆心角、弧、弦的关系,等边三角形的判定与性质
专题：
分析：（1）根据
=
=
，可得出AB=BC=AC，即可得出三角形的形状；
（2）过点O作OD⊥BC，垂足为D，连接OC，根据直角三角形的性质即可得出⊙O的半径．
 |
| AB |
|
| BC |
|
| CA |
（2）过点O作OD⊥BC，垂足为D，连接OC，根据直角三角形的性质即可得出⊙O的半径．
解答：解：（1）∵
=
=
，
∴AB=BC=AC，
∴△ABC为等边三角形；
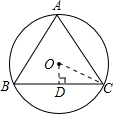（2）过点O作OD⊥BC，垂足为D，连接OC，
∴CD=
BC=
a，
∵△ABC为等边三角形，
∴∠ACB=60°，
∴∠OCD=30°，
设OD=x，则OC=2x，
∴OD2+CD2=OC2，
∴x2+
a2=4x2，
∴x=
a，
∴⊙O的半径为
．
|
| AB |
|
| BC |
|
| CA |
∴AB=BC=AC，
∴△ABC为等边三角形；
（2）过点O作OD⊥BC，垂足为D，连接OC，∴CD=
| 1 |
| 2 |
| 1 |
| 2 |
∵△ABC为等边三角形，
∴∠ACB=60°，
∴∠OCD=30°，
设OD=x，则OC=2x，
∴OD2+CD2=OC2，
∴x2+
| 1 |
| 4 |
∴x=
| ||
| 6 |
∴⊙O的半径为
| ||
| 3 |
点评：本题考查了圆心角、弧、弦以及等边三角形的性质，直角三角形的性质和勾股定理，是一道综合性较强的题目，难度不大．
练习册系列答案
相关题目
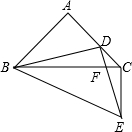如图，Rt△ABC中，∠BAC=90°，AB=AC，AC边上有点D，连接BD，以BD为腰作等腰直角三角形BDE，DE交BC于F，那么下面结论：①△ABD∽△CBE，②∠BCE=90°，③DF•EF=BF•CF，④BC-CE=
如图，已知直线y=-x+4与反比例函数y=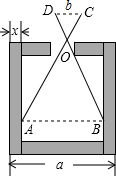
如图，已知零件的外径a=35cm，要求它的厚度x，需先求出内孔的直径AB，但不能直接量出AB，现用一个交叉卡钳（两条尺长AC和BD相等）测量，已知OA：OC=OB：OD=3，且量得CD=10cm，求厚度x．