题目内容
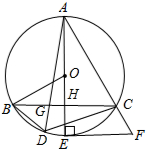 如图,AE为⊙O的直径,EF为⊙O的切线,E为切点,连接AF交⊙O于点C,CB∥EF交AE于H交⊙O于B,D为BC弧上一点,连接AD交BC于G.
如图,AE为⊙O的直径,EF为⊙O的切线,E为切点,连接AF交⊙O于点C,CB∥EF交AE于H交⊙O于B,D为BC弧上一点,连接AD交BC于G.(1)求证:AD平分∠BDC;
(2)若BC垂直平分OE,BD=2,DC=4,求⊙O的半径.
考点:切线的性质
专题:证明题
分析:(1)根据切线的性质,由EF为⊙O的切线得到AE⊥EF,而BC∥EF,根据平行线的性质得AE⊥BC,根据垂直定理得
=
,然后根据圆周角得到∠ADB=∠ADC;
(2)连接AB,作BM⊥CD于M,如图,由于BC垂直平分OE易得OH=
OB,所以∠OBH=30°,可计算出∠BOH=60°,根据圆周角定理得∠BAC=60°,在根据圆内接四边形的性质得∠BDM=∠BAC=60°,根据含30度的直角三角形三边的关系得DM=
BD=1,BM=
DM=
,然后在Rt△BCM中根据勾股定理计算BC的长.
 |
| AB |
 |
| AC |
(2)连接AB,作BM⊥CD于M,如图,由于BC垂直平分OE易得OH=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
解答:(1)证明:∵EF为⊙O的切线,
∴AE⊥EF,
∵BC∥EF,
∴AE⊥BC,
∴
=
,
∴∠ADB=∠ADC,
即AD平分∠BDC;
(2)解:连接AB,作BM⊥CD于M,如图,
∵BC垂直平分OE,
∴OH=EH,
∴OH=
OB,
∴∠OBH=30°,
∴∠BOH=60°,
∴∠BAC=60°,
∴∠BDM=∠BAC=60°,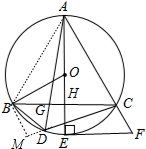
在Rt△BDM中,∵∠MBD=30°,
∴DM=
BD=1,BM=
DM=
,
在Rt△BCM中,∵CM=CD+DM=4+1=5,BM=
,
∴BC=
=2
.
∴BH=
,
设OH=x,则OB=2x,
∴x2+(
)2=(2x)2,
∴x=
,
∴半径为:
.
∴AE⊥EF,
∵BC∥EF,
∴AE⊥BC,
∴
 |
| AB |
 |
| AC |
∴∠ADB=∠ADC,
即AD平分∠BDC;
(2)解:连接AB,作BM⊥CD于M,如图,
∵BC垂直平分OE,
∴OH=EH,
∴OH=
| 1 |
| 2 |
∴∠OBH=30°,
∴∠BOH=60°,
∴∠BAC=60°,
∴∠BDM=∠BAC=60°,

在Rt△BDM中,∵∠MBD=30°,
∴DM=
| 1 |
| 2 |
| 3 |
| 3 |
在Rt△BCM中,∵CM=CD+DM=4+1=5,BM=
| 3 |
∴BC=
| BM2+CM2 |
| 7 |
∴BH=
| 7 |
设OH=x,则OB=2x,
∴x2+(
| 7 |
∴x=
| ||
| 3 |
∴半径为:
2
| ||
| 3 |
点评:本题考查了圆的切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.也考查了勾股定理.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知二次函数y=ax2+bx+c,且ac<0,则它的图象经过( )
| A、一、二、三象限 |
| B、二、三、四象限 |
| C、一、三、四象限 |
| D、一、二、三、四象限 |
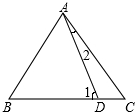 如图,已知AB=AC=BD,那么( )
如图,已知AB=AC=BD,那么( )| A、∠1=∠2 |
| B、2∠1+∠2=180° |
| C、∠1+3∠2=180° |
| D、3∠1-∠2=180° |
 如图,已知直线y=-x+4与反比例函数y=
如图,已知直线y=-x+4与反比例函数y=