题目内容
 如图,长方形ABCD沿AE折叠,使点B落在CD边上的点F处,如果∠EFC=60°,那么∠BAE等于多少度?请说明理由.
如图,长方形ABCD沿AE折叠,使点B落在CD边上的点F处,如果∠EFC=60°,那么∠BAE等于多少度?请说明理由.考点:直角三角形的性质,角的计算,翻折变换(折叠问题)
专题:
分析:根据直角三角形两锐角互余求出∠CEF,再根据翻折的性质求出∠AED,根据直角三角形两锐角互余求出∠DAE,然后根据∠BAE=∠BAD-∠DAE计算即可得解.
解答:解:∠BAE=75°.
理由如下:∵∠EFC=60°,
∴∠CEF=90°-60°=30°,
由翻折的性质得,∠AED=∠AEF=
(180°-∠CEF)=
(180°-30°)=75°,
∴∠DAE=90°-75°=25°,
∴∠BAE=∠BAD-∠DAE=90°-25°=75°,
即∠BAE=75°.
理由如下:∵∠EFC=60°,
∴∠CEF=90°-60°=30°,
由翻折的性质得,∠AED=∠AEF=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠DAE=90°-75°=25°,
∴∠BAE=∠BAD-∠DAE=90°-25°=75°,
即∠BAE=75°.
点评:本题考查了直角三角形的性质,角的计算,翻折变换的性质,熟记各性质并准确识图理清图中各角度之间的关系是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如图,是用火柴棒按规律拼成的图形,则第6个图形中一共有( )个平行四边形.

| A、6 | B、7 | C、8 | D、9 |
已知a、b是两个相邻的整数,且满足a<
<b,则a+b的值为( )
| 13 |
| A、25 | B、16 | C、9 | D、7 |
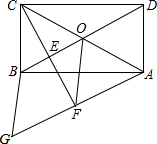 如图,在矩形ABCD中,AC、BD相交于点O,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BO,连接BG、DF.若AG=13,CF=6,求四边形BOFG的周长.
如图,在矩形ABCD中,AC、BD相交于点O,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BO,连接BG、DF.若AG=13,CF=6,求四边形BOFG的周长.