题目内容
计算:
(1)(-1)0+2-2-(-1)2012;
(2)(2x2y)2•(-6xy4)÷(24x4y5);
(3)用整式的乘法公式计算:20002-2001×1999.
(1)(-1)0+2-2-(-1)2012;
(2)(2x2y)2•(-6xy4)÷(24x4y5);
(3)用整式的乘法公式计算:20002-2001×1999.
考点:整式的混合运算
专题:计算题
分析:(1)原式第一项利用零指数幂法则计算,第二项利用负指数幂法则计算,最后一项利用-1的偶次幂为1计算即可得到结果;
(2)原式利用幂的乘方及积的乘方运算法则计算,再利用单项式乘除单项式法则计算即可得到结果;
(3)原式变形后,利用平方差公式化简,去括号合并即可得到结果.
(2)原式利用幂的乘方及积的乘方运算法则计算,再利用单项式乘除单项式法则计算即可得到结果;
(3)原式变形后,利用平方差公式化简,去括号合并即可得到结果.
解答:解:(1)原式=1+
-1=
;
(2)原式=4x4y2•(-6xy4)÷(24x4y5)=-24x5y6÷24x4y5=-xy;
(3)原式=20002-2001×1999=20002-(2000+1)×(2000-1)=20002-(20002-1)=1.
| 1 |
| 4 |
| 1 |
| 4 |
(2)原式=4x4y2•(-6xy4)÷(24x4y5)=-24x5y6÷24x4y5=-xy;
(3)原式=20002-2001×1999=20002-(2000+1)×(2000-1)=20002-(20002-1)=1.
点评:此题考查了整式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
如果(2x+m)(x-5)展开后的结果中不含有x的一次项,那么m等于( )
| A、5 | B、-10 | C、-5 | D、10 |
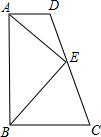 如图,四边形ABCD中,AD∥BC,点E是CD的中点,连接AE、BE,∠EAD=∠EAB.给出下列五个结论:
如图,四边形ABCD中,AD∥BC,点E是CD的中点,连接AE、BE,∠EAD=∠EAB.给出下列五个结论: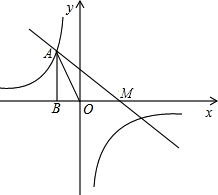 如图,已知反比例函数y=
如图,已知反比例函数y= 如图,在正方形ABCD中,边AB上有一点M,其中AM=3BM,N是AD上一点,且AN=ND,判断△MNC是否是直角三角形,并说明理由.
如图,在正方形ABCD中,边AB上有一点M,其中AM=3BM,N是AD上一点,且AN=ND,判断△MNC是否是直角三角形,并说明理由.