题目内容
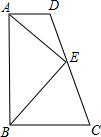 如图,四边形ABCD中,AD∥BC,点E是CD的中点,连接AE、BE,∠EAD=∠EAB.给出下列五个结论:
如图,四边形ABCD中,AD∥BC,点E是CD的中点,连接AE、BE,∠EAD=∠EAB.给出下列五个结论:①BE⊥AE;②BE平分∠ABC;③AD+BC=AB;④AB⊥BC;⑤△ABC=
| 1 |
| 2 |
其中正确的有( )
| A、2 | B、3 | C、4 | D、5 |
考点:四边形综合题
专题:压轴题
分析:延长AE交BC延长线于M,求出∠EAB=∠M,推出AB=BM,AD=CM,AE=EM,即可推出①②③正确,根据三角形的面积公式即可判断⑤;根据AE和BE平分∠DAB、∠ABC即可判断④.
解答: 解:延长AE交BC延长线于M,
解:延长AE交BC延长线于M,
∵AD∥BC,
∴∠DAE=∠M,
∵∠EAD=∠EAB,
∴∠EAB=∠M,
∴AB=BM,
∵E为CD中点,
∴DE=ECC,
∵AD∥BC,
∴△DAE∽△CME,
∴
=
=
,
∴AD=CM,AE=EM,
∴AD+BC=AB,
∵AB=BM,AE=EM,
∴BE⊥AE;BE平分∠ABC;
∴∠ABE=∠CBE,
连接AC,
∵AD≠BC,
∴S△ABC≠S△ADC,
∴S△ABC=
S四边形ABCD错误;
∵AD≠BC,AE平分∠DAB,BE平分∠ABC,
∴∠DAE=∠EAB,∠ABE=∠CBE,
∴不能推出AB⊥BC,
即①②③正确;④⑤错误;
故选B.
 解:延长AE交BC延长线于M,
解:延长AE交BC延长线于M,∵AD∥BC,
∴∠DAE=∠M,
∵∠EAD=∠EAB,
∴∠EAB=∠M,
∴AB=BM,
∵E为CD中点,
∴DE=ECC,
∵AD∥BC,
∴△DAE∽△CME,
∴
| AD |
| CM |
| DE |
| CE |
| AE |
| EM |
∴AD=CM,AE=EM,
∴AD+BC=AB,
∵AB=BM,AE=EM,
∴BE⊥AE;BE平分∠ABC;
∴∠ABE=∠CBE,
连接AC,

∵AD≠BC,
∴S△ABC≠S△ADC,
∴S△ABC=
| 1 |
| 2 |
∵AD≠BC,AE平分∠DAB,BE平分∠ABC,
∴∠DAE=∠EAB,∠ABE=∠CBE,
∴不能推出AB⊥BC,
即①②③正确;④⑤错误;
故选B.
点评:本题考查了相似三角形的性质和判断,平行线的性质,等腰三角形的性质和判定的应用,关键是推出△ABM是等腰三角形,题目是一道比较常见的题目,比较典型.

练习册系列答案
相关题目
下列各式中,正确的是( )
A、
| |||
B、±
| |||
C、
| |||
D、
|
为了解2014年洛阳市九年级学生的数学成绩,从中随机抽取了1000名学生进行调查.下列说法错误的( )
| A、2014年洛阳市全体九年级学生是总体 |
| B、每一名学生的数学成绩是个体 |
| C、抽取的1000名学生的成绩是总体的一个样本 |
| D、样本容量是1000 |
直角三角形的三边分别加1后,所得到的图形是( )
| A、直角三角形 | B、锐角三角形 |
| C、钝角三角形 | D、无法判断 |
 实数a、b在数轴上的对应点如图,化简
实数a、b在数轴上的对应点如图,化简| a2 |
| b2 |
| (a-b)2 |
| A、2a-2b | B、0 |
| C、-2a | D、2b |
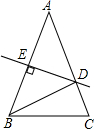 如图,△ABC是等腰三角形,且顶角∠A=36°,DE是AB的垂直平分线,则有:
如图,△ABC是等腰三角形,且顶角∠A=36°,DE是AB的垂直平分线,则有: