如图.△ABC中.∠ACB=90°.AB=$\sqrt{8}$.BC=$\sqrt{2}$.求△ABC的面积．题目和参考答案——青夏教育精英家教网—

题目内容

18．

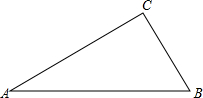如图，△ABC中，∠ACB=90°，AB=$\sqrt{8}$，BC=$\sqrt{2}$，求△ABC的面积．

分析根据勾股定理求出AC，由直角三角形的面积公式即可求出结果．

解答解：∵∠ACB=90°，AB=$\sqrt{8}$，BC=$\sqrt{2}$，
∴AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=$\sqrt{6}$，
∴△ABC的面积=$\frac{1}{2}$AC•BC=$\frac{1}{2}$×$\sqrt{6}$×$\sqrt{2}$=$\sqrt{3}$．

点评本题考查的是勾股定理的运用、三角形面积的计算；熟练掌握勾股定理是解决问题的关键．

练习册系列答案

相关题目

8．如果方程$\sqrt{x}$-a=2无实数解，那么a的取值范围是a＜-2．

9．已知|2x+1|+（y-2）²=0，求（xy）²⁰¹¹的值．

6．下列按规律排列的数：1、$\frac{1}{2}$、$\frac{1}{4}$、$\frac{1}{8}$、$\frac{1}{16}$…第2015个数应是（　　）

（$\frac{1}{2}$）²⁰¹⁴

（$\frac{1}{2}$）²⁰¹⁵

（$\frac{1}{2}$）²⁰¹⁶

13．下列判断：
①有两边及其中一边上的高对应相等的两个三角形全等；
②有两边及第三边上的高对应相等的两个三角形全等；
③三角形有6个边、角元素中，有5个元素分别对应相等的两个三角形全等；
④一边及其他两边上的高对应相等的两个三角形全等，
其中成立的是（　　）

3．若关于x的多项式-5x³-（m+2）x²+（3-n）x-1不含二次项和一次项．则mⁿ的值为-8．

10．下列四个选项中，计算结果最大的是（　　）

7．已知x，y为有理数，如果规定一种新运算*，其意义是x*y=xy+1，试根据这种运算完成下列各题．
（1）求2*4的值；
（2）求1*4*0的值；
（3）任意选取两个有理数（至少一个为负数）分别填入下列□与○内，并比较两个运算结果，你能发现什么？□*○与○*□；
（4）根据以上方法，设a，b，c为有理数，请与其他同学交流a*（b+c）与a*b+a*c的关系，并用式子把它们表达出来．

8．

如图，△ABC中，DE是AC的垂直平分线，AE=3cm，△ABD的周长为11cm，求△ABC的周长．

试题分类