题目内容
3．若关于x的多项式-5x3-（m+2）x2+（3-n）x-1不含二次项和一次项．则mn的值为-8．分析 先确定二次项及一次项的系数，再令其为0即可求m，n的值即可．
解答 解：
∵多项式-5x3-（m+2）x2+（3-n）x-1不含二次项和一次项，
∴-（m+2）=0，（3-n）=0，
解得m=-2，n=3，
∴mn=（-2）3=-8，
故答案为：-8．
点评 本题考查了多项式和代数式求值，在多项式中不含哪一项，即哪一项的系数为0，两项的系数互为相反数，合并同类项时为0．
练习册系列答案
相关题目
13．下面关于函数的三种表示方法叙述错误的是（ ）
| A． | 用图象法表示函数关系，可以直观地看出因变量如何随着自变量而变化 | |
| B． | 用列表法表示函数关系，可以很清楚地看出自变量取的值与因变量的对应值 | |
| C． | 用公式法表示函数关系，可以方便地计算函数值 | |
| D． | 任何函数关系都可以用上述三种方法来表示 |
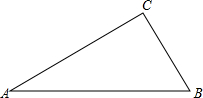如图，△ABC中，∠ACB=90°，AB=$\sqrt{8}$，BC=$\sqrt{2}$，求△ABC的面积．
如图，将长方形纸片沿AC折叠，使点B落在点B′处，再沿CF折叠使CE边与CB′重合，得到∠ACF．猜想∠ACF的度数．并说说你的理由．