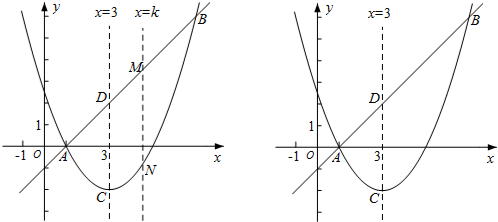题目内容
如图，顶点为A（1，4）的抛物线与y轴交于点B（0，2），与x轴交于C，D两点，抛物线上一动点P沿抛物线从点C向点A运动，点P关于抛物线对称轴的对称点为点Q，分别过点P，Q向x轴作垂线，垂足分别为点M，N．抛物线对称轴与x轴相交于点E．（1）求此抛物线的解析式；
（2）是否存在点P，使得△ACE与△PMQ相似？若存在，请求出点P的坐标；若不存在，请说明理由．
考点：二次函数综合题
专题：
分析：（1）设此抛物线的解析式为：y=a（x-h）2+k，由已知条件可知，h和k的值，再把B的坐标代入求出a的值即可；
（2）假设存在点P，使得△ACE与△PMQ相似，不妨设点P（1-t，4-2t2），由抛物线的对称性可求出点Q的坐标为（1+t，4-2t2），再分两种情况△ACE∽△PMQ或△ACE∽△QMP讨论求出符合题意的t值即可．
（2）假设存在点P，使得△ACE与△PMQ相似，不妨设点P（1-t，4-2t2），由抛物线的对称性可求出点Q的坐标为（1+t，4-2t2），再分两种情况△ACE∽△PMQ或△ACE∽△QMP讨论求出符合题意的t值即可．
解答：解：（1）设此抛物线的解析式为：y=a（x-h）2+k，
∵顶点为A（1，4）
∴此抛物线的解析式为：y=a（x-1）2+4，
将点B（0，2）代入可求得：a=-2，
∴此抛物线的解析式为：y=-2（x-1）2+4=-2x2+4x+2．
（2）假设存在点P，使得△ACE与△PMQ相似，不妨设点P（1-t，4-2t2），
根据对称性可得，点Q的坐标为（1+t，4-2t2），
令y=4-2（x-1）2=0，
解得到：x=1±
，
从而有：C（1-
），D（1+
，0）
所以：0＜t＜
，
由于△ACE与△PMQ相似，
则必有：
=
或
=
，
当
=
得到
=
，
解得t=2-
或-2-
（舍去）
从而得到点P（
-1，8
-8）．
当
=
得到
=
，
解得t=
或
（舍去），
从而得到点P（
，
），
故存在这样的点P，坐标为（
-1，8
-8）或（
，
）．
∵顶点为A（1，4）
∴此抛物线的解析式为：y=a（x-1）2+4，
将点B（0，2）代入可求得：a=-2，
∴此抛物线的解析式为：y=-2（x-1）2+4=-2x2+4x+2．
（2）假设存在点P，使得△ACE与△PMQ相似，不妨设点P（1-t，4-2t2），
根据对称性可得，点Q的坐标为（1+t，4-2t2），
令y=4-2（x-1）2=0，
解得到：x=1±
| 2 |
从而有：C（1-
| 2 |
| 2 |
所以：0＜t＜
| 2 |
由于△ACE与△PMQ相似，
则必有：
| PM |
| PQ |
| AE |
| CE |
| PM |
| PQ |
| CE |
| AE |
当
| PM |
| PQ |
| AE |
| CE |
| 4-2t2 |
| 2t |
| 4 | ||
|
解得t=2-
| 2 |
| 2 |
从而得到点P（
| 2 |
| 2 |
当
| PM |
| PQ |
| CE |
| AE |
| 4-2t2 |
| 2t |
| ||
| 4 |
解得t=
| ||||
| 8 |
-
| ||||
| 8 |
从而得到点P（
8+
| ||||
| 8 |
-17-4
| ||||||
| 8 |
故存在这样的点P，坐标为（
| 2 |
| 2 |
8+
| ||||
| 8 |
-17-4
| ||||||
| 8 |
点评：本题是二次函数的综合题型，其中涉及到的知识点有抛物线的顶点公式、相似三角形的判定和性质以及解一元二次方程的问题．在求有关动点问题时要注意分析题意分情况讨论结果．
练习册系列答案
相关题目
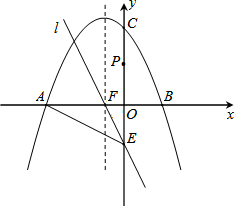如图，抛物线C1：y=ax2+bx+4的图象与两坐标轴分别交于A、B、C三点，经过点E（0，-2）的直线l：y=kx-2（k≠0）与x轴、抛物线的对称轴x=-1交于点F．
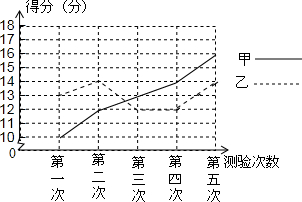甲乙两人参加某体育项目训练，近期的五次测验得分情况（单位：分）如图所示
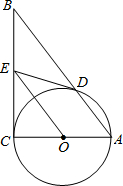如图在Rt△ABC中，∠C=90°，以AC为直径作⊙O，交AB于D，过O作OE∥AB，交BC于E．