题目内容
2.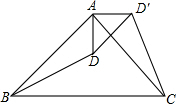 如图,△ABC是等腰直角三角形,BC是斜边,将△ABD绕点A逆时针旋转后,能与△ACD′重合.如果AD=2,那么DD′=2$\sqrt{2}$.
如图,△ABC是等腰直角三角形,BC是斜边,将△ABD绕点A逆时针旋转后,能与△ACD′重合.如果AD=2,那么DD′=2$\sqrt{2}$.
分析 如图,首先运用翻折变换的性质求出∠DAD′=90°,AD=AD′=2;其次运用勾股定理求出DD′的长,即可解决问题.
解答  解:如图,由题意得:
解:如图,由题意得:
∠DAD′=∠BAC=90°,AD=AD′=2,
∴由勾股定理得:DD′2=AD2+AD′2,
∴DD′=2$\sqrt{2}$,
故答案为2$\sqrt{2}$.
点评 该题主要考查了翻折变换的性质、勾股定理等几何知识点及其应用问题;应牢固掌握翻折变换的性质、勾股定理等几何知识点,这是灵活运用、解题的基础和关键.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
12.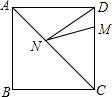 如图,正方形ABCD的边长为8,M在DC上,且DM=2,N是AC上一动点,则DN+MN的最小值为( )
如图,正方形ABCD的边长为8,M在DC上,且DM=2,N是AC上一动点,则DN+MN的最小值为( )
 如图,正方形ABCD的边长为8,M在DC上,且DM=2,N是AC上一动点,则DN+MN的最小值为( )
如图,正方形ABCD的边长为8,M在DC上,且DM=2,N是AC上一动点,则DN+MN的最小值为( )| A. | 6 | B. | 8 | C. | 12 | D. | 10 |
14.顺次连接等腰梯形各边中点所得到的四边形一定是( )
| A. | 正方形 | B. | 菱形 | C. | 矩形 | D. | 等腰梯形 |
12.把多项式2x2-8分解因式,结果正确的是( )
| A. | 2(x2-8) | B. | 2(x-2)2 | C. | 2(x+2)(x-2) | D. | 2x(x-$\frac{4}{x}$) |
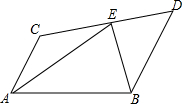 如图,已知梯形ABCD,AC∥BD,点E在CD上,有下列五个条件:
如图,已知梯形ABCD,AC∥BD,点E在CD上,有下列五个条件: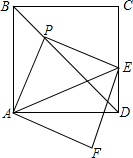 如图,点P为正方形ABCD的对角线BD上的一个动点(不与B,D重合),过点P作PE⊥AP交射线CD于点E,过点E作EF⊥PE交AP的垂线AF于点F.
如图,点P为正方形ABCD的对角线BD上的一个动点(不与B,D重合),过点P作PE⊥AP交射线CD于点E,过点E作EF⊥PE交AP的垂线AF于点F.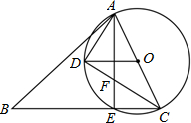 如图,在锐角△ABC中,AC是最短边,以AC的中点O为圆心,$\frac{1}{2}$AC长为半径作⊙O,交BC于点E,过O作OD∥BC交⊙O于点D,连结AE、AD、DC.
如图,在锐角△ABC中,AC是最短边,以AC的中点O为圆心,$\frac{1}{2}$AC长为半径作⊙O,交BC于点E,过O作OD∥BC交⊙O于点D,连结AE、AD、DC.