题目内容
5.阅读下列因式分解的过程,再回答所提出的问题:1+x+x(x+1)+x(x+1)2
(1+x)[1+x+x(x+1)]
=(1+x)2(1+x)
=(1+x)3
(1)上述分解因式的方法是提公因式法,共应用了2次.
(2)若分解1+x+x(x+1)+x(x+1)2+x(x+1)3,则需应用上述方法3次,结果是(x+1)4.
(3)分解因式:1+x+x(x+1)+x(x+1)2…+x(x+1)n(n为正整数)的结果是(x+1)n+1.
分析 (1)根据已知材料直接回答即可;
(2)利用已知材料进而提取公因式(1+x),进而得出答案;
(3)利用已知材料提取公因式进而得出答案.
解答 解:(1)上述分解因式的方法是:提公因式法,共应用了2次.
故答案为:提公因式法,2次;
(2)1+x+x(x+1)+x(x+1)2+x(x+1)3,
=(1+x)[1+x+x(1+x)+x(1+x)2]
=(1+x)(1+x)[1+x+x(1+x)]
=(1+x)2(1+x)(1+x)
=(1+x)4,
故分解1+x+x(x+1)+x(x+1)2+x(x+1)3,则需应用上述方法3次,结果是:(x+1)4.
(3)分解因式:1+x+x(x+1)+x(x+1)2…+x(x+1)n(n为正整数)的结果是:(x+1)n+1.
故答案为:(x+1)n+1.
点评 此题主要考查了提取公因式法分解因式,正确提取公因式是解题关键.

练习册系列答案
相关题目
15.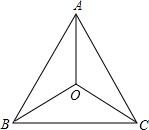 如图,O是正△ABC三条角平分线的交点.则下列说法错误的是( )
如图,O是正△ABC三条角平分线的交点.则下列说法错误的是( )
 如图,O是正△ABC三条角平分线的交点.则下列说法错误的是( )
如图,O是正△ABC三条角平分线的交点.则下列说法错误的是( )| A. | △AOC与△BOC关于直线OC对称 | |
| B. | △AOC绕O点逆时针旋转240°与△COB重合 | |
| C. | △AOC绕O点顺时针旋转120°与△COB重合 | |
| D. | △AOC只通过平移就能与△BOC重合 |
13.下列长度的各组线段中,能够组成直角三角形的是( )
| A. | 8,15,17 | B. | 7,20,25 | C. | 5,11,12 | D. | 5,6,7 |
20.下列判断正确的是( )
| A. | 有一条直角边对应相等的两个直角三角形全等 | |
| B. | 腰长相等的两个等腰三角形全等 | |
| C. | 斜边相等的两个等腰直角三角形全等 | |
| D. | 两个锐角对应相等的两个直角三角形全等 |
 将两张矩形纸片如图摆放,其中一矩形顶点落在另一矩形的边上,则∠1+∠2等于90°.
将两张矩形纸片如图摆放,其中一矩形顶点落在另一矩形的边上,则∠1+∠2等于90°. 如图,直线AB,CD分别与直线AC相交于点A,C,与直线BD相交于点B,D.若∠1=∠2,∠3=75°,求∠4、∠5的度数.
如图,直线AB,CD分别与直线AC相交于点A,C,与直线BD相交于点B,D.若∠1=∠2,∠3=75°,求∠4、∠5的度数. 如图,直线a∥b,∠1=120°,则∠2=120度.
如图,直线a∥b,∠1=120°,则∠2=120度. 如图,直线l:y=-$\frac{3}{4}$x+3与x轴交于点A,与y轴交于点B.
如图,直线l:y=-$\frac{3}{4}$x+3与x轴交于点A,与y轴交于点B.