题目内容
2.下列计算中正确的是( )| A. | $\frac{1}{3}$+$\frac{1}{2}$=$\frac{2}{5}$ | B. | $\root{3}{-27}$=3 | C. | a10=(a5)2 | D. | b-2=-b2 |
分析 A、根据有理数的加法进行判定;B、根据立方根进行判定、C、根据幂的乘方进行判定;D、根据负整数指数幂即可解答.
解答 解:A、$\frac{1}{3}+\frac{1}{2}=\frac{5}{6}$,故错误;
B、$\root{3}{-27}$=-3,故错误;
C、a10=(a5)2,正确;
D、${b}^{-2}=\frac{1}{{b}^{2}}$,故错误;
故选:C.
点评 本题考查了立方根、幂的乘方,解决本题的关键是熟记立方根、幂的乘方.

练习册系列答案
相关题目
12.已知二次三项式x2-kx-15能分解成系数为整数的两个一次因式的积,则整数k的取值范围有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
13.某省2013年的快递业务量为1.5亿件,受益于电子商务发展和法治环境改善等多重因素,快递业务迅猛发展.若2015年的快递业务量达到4.5亿件.设2014年与2013年这两年的平均增长率为x,则下列方程正确的是( )
| A. | 1.5(1+x)=4.5 | B. | 1.5(1+2x)=4.5 | ||
| C. | 1.5(1+x)2=4.5 | D. | 1.5(1+x)+1.4(1+x)2=4.5 |
17.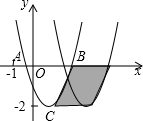 如图,已知抛物线y=ax2+bx+c与轴交于A、B两点,顶点C的纵坐标为-2,现将抛物线向右平移2个单位,得到抛物线y=a1x2+b1x+c1,则下列结论:
如图,已知抛物线y=ax2+bx+c与轴交于A、B两点,顶点C的纵坐标为-2,现将抛物线向右平移2个单位,得到抛物线y=a1x2+b1x+c1,则下列结论:
①b>0;②a-b+c<0;③阴影部分的面积为4;④若c=-1,则b2=4a.
正确的是( )
 如图,已知抛物线y=ax2+bx+c与轴交于A、B两点,顶点C的纵坐标为-2,现将抛物线向右平移2个单位,得到抛物线y=a1x2+b1x+c1,则下列结论:
如图,已知抛物线y=ax2+bx+c与轴交于A、B两点,顶点C的纵坐标为-2,现将抛物线向右平移2个单位,得到抛物线y=a1x2+b1x+c1,则下列结论:①b>0;②a-b+c<0;③阴影部分的面积为4;④若c=-1,则b2=4a.
正确的是( )
| A. | ①③ | B. | ②③ | C. | ②④ | D. | ③④ |
11.以a,b,c为边长的下列三角形,能判定是直角三角形的有( )
①a:b:c=1:1:$\sqrt{2}$;
②a,b,c满足a2-b2=c2;
③a=m2+n2,b=mn,c=m2-n2(m>n>0);
④a=1,b=2,c=$\sqrt{3}$.
①a:b:c=1:1:$\sqrt{2}$;
②a,b,c满足a2-b2=c2;
③a=m2+n2,b=mn,c=m2-n2(m>n>0);
④a=1,b=2,c=$\sqrt{3}$.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
9.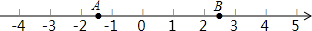 如图,数轴上两点A、B表示的数可能是( )
如图,数轴上两点A、B表示的数可能是( )
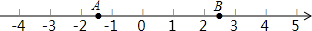 如图,数轴上两点A、B表示的数可能是( )
如图,数轴上两点A、B表示的数可能是( )| A. | -1.5和2.5 | B. | -2.5和2.5 | C. | -1.5和3.5 | D. | -2.5和3.5 |