题目内容
10.(1)化简:$\frac{4}{{{a^2}-4}}-\frac{1}{a-2}$(2)解方程:$\frac{x}{x-1}$-1=$\frac{3}{(x-1)(x+2)}$.
分析 (1)原式两项通分并利用同分母分式的减法法则计算即可得到结果;
(2)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:(1)原式=$\frac{4}{(a+2)(a-2)}$-$\frac{a+2}{(a+2)(a-2)}$=$\frac{4-(a+2)}{{({a+2})({a-2})}}$=$\frac{2-a}{{({a+2})({a-2})}}$=-$\frac{1}{a+2}$;
(2)去分母得:x(x+2)-(x-1)(x+2)=3,
解得:x=1,
检验:x=1是增根,
则原方程无解.
点评 此题考查了解分式方程,熟练掌握运算法则是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
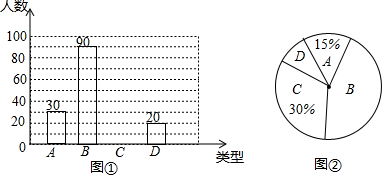
18.某中学八年级(8)班同学全部参加课外活动情况统计如图:

(1)请你根据以上统计中的信息,填写下表:
(2)补全条形统计图;
(3)若该学校八年级共有600名学生,根据统计图结果估计八年级参加排球活动项目的学生共有168名.

(1)请你根据以上统计中的信息,填写下表:
| 该班人数 | 这五个活动项目人数的中位数 | 这五个活动项目人数的平均数 |
| 50 | 9 | 10 |
(3)若该学校八年级共有600名学生,根据统计图结果估计八年级参加排球活动项目的学生共有168名.
5.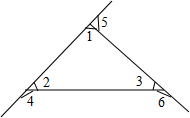 如图所示,有下列五种说法:①∠1和∠4是同位角;②∠3和∠5是内错角;③∠2和∠6是同旁内角;④∠5和∠2是同位角;⑤∠1和∠3是同旁内角;其中正确的是( )
如图所示,有下列五种说法:①∠1和∠4是同位角;②∠3和∠5是内错角;③∠2和∠6是同旁内角;④∠5和∠2是同位角;⑤∠1和∠3是同旁内角;其中正确的是( )
 如图所示,有下列五种说法:①∠1和∠4是同位角;②∠3和∠5是内错角;③∠2和∠6是同旁内角;④∠5和∠2是同位角;⑤∠1和∠3是同旁内角;其中正确的是( )
如图所示,有下列五种说法:①∠1和∠4是同位角;②∠3和∠5是内错角;③∠2和∠6是同旁内角;④∠5和∠2是同位角;⑤∠1和∠3是同旁内角;其中正确的是( )| A. | ①②③ | B. | ①②③④ | C. | ①②③④⑤ | D. | ①②④⑤ |
 画图:已知△ABC,试将其沿着箭头方向平移2厘米的长度.
画图:已知△ABC,试将其沿着箭头方向平移2厘米的长度.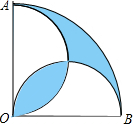 如图,在圆心角为直角的扇形OAB中,分别以OA、OB为直径作两个半圆,向直角扇形OAB内随机取一点,则该点刚好来自阴影部分的概率是1-$\frac{2}{π}$.
如图,在圆心角为直角的扇形OAB中,分别以OA、OB为直径作两个半圆,向直角扇形OAB内随机取一点,则该点刚好来自阴影部分的概率是1-$\frac{2}{π}$.