题目内容
20.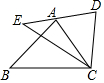 如图所示,△ABC≌△DEC,∠ACB=60°,∠BCD=100°,点A恰好落在线段ED上,则∠B的度数为( )
如图所示,△ABC≌△DEC,∠ACB=60°,∠BCD=100°,点A恰好落在线段ED上,则∠B的度数为( )| A. | 50° | B. | 60° | C. | 55° | D. | 65° |
分析 根据全等三角形对应角相等可得∠DCE=∠ACB,AC=CD,∠D=∠BAC,求出∠D=∠DAC,然后求出∠ACD,根据三角形内角和定理求出∠D,求出∠BAC,根据三角形内角和定理求出即可.
解答 解:∵△ABC≌△DEC,
∴∠DCE=∠ACB=60°,AC=CD,∠D=∠BAC,
∴∠D=∠DAC,
∵∠BCD=100°,∠ACB=60°,
∴∠ACD=∠BCD-∠ACB=100°-60°=40°,
∴∠BAC=∠D=$\frac{1}{2}$×(180°-40°)=70°,
∴∠B=180°-∠ACB-∠BAC=180°-70°-60°=50°,
故选A.
点评 本题考查了全等三角形对应角相等,对应边相等的性质,也考查了三角形内角和定理等于180°,熟记性质并准确识图,理清图中各角度之间的关系是解题的关键.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
11.观察下列各式数:-2x,4x2,-8x3,16x4,-32x5,…则第n个式子是( )
| A. | -2n-1xn | B. | (-2)n-1xn | C. | -2nxn | D. | (-2)nxn |
8.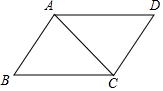 如图,已知AB∥CD,AD∥CB,则△ABC≌△CDA的依据是( )
如图,已知AB∥CD,AD∥CB,则△ABC≌△CDA的依据是( )
 如图,已知AB∥CD,AD∥CB,则△ABC≌△CDA的依据是( )
如图,已知AB∥CD,AD∥CB,则△ABC≌△CDA的依据是( )| A. | SAS | B. | ASA | C. | AAS | D. | SSS |
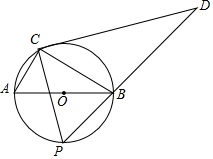 如图,⊙O的直径为4,C为⊙O上一个定点,∠ABC=30°,动点P从A点出发沿半圆弧$\widehat{AB}$向B点运动(点P与点C在直径AB的异侧),当P点到达B点时运动停止,在运动过程中,过点C作CP的垂线CD交PB的延长线于D点.
如图,⊙O的直径为4,C为⊙O上一个定点,∠ABC=30°,动点P从A点出发沿半圆弧$\widehat{AB}$向B点运动(点P与点C在直径AB的异侧),当P点到达B点时运动停止,在运动过程中,过点C作CP的垂线CD交PB的延长线于D点. 如图,要设计一幅长为60cm,宽为40cm的矩形图案,其中有两横两竖的矩形彩条,横竖彩条宽度比为1:2,若彩条所占面积是图案面积的一半,求一条横彩条的宽度.
如图,要设计一幅长为60cm,宽为40cm的矩形图案,其中有两横两竖的矩形彩条,横竖彩条宽度比为1:2,若彩条所占面积是图案面积的一半,求一条横彩条的宽度.