题目内容
8. 如图,四边形ABCD的对角线AC与BD相交于点O,AB=AD,CB=CD.求证:
如图,四边形ABCD的对角线AC与BD相交于点O,AB=AD,CB=CD.求证:(1)△ABC≌△ADC;
(2)AC垂直平分BD.
分析 (1)根据SSS定理推出即可;
(2)根据全等三角形的性质得出∠BAC=∠DAC,根据等腰三角形的性质得出即可.
解答 证明:(1)∵在△ABC与△ADC中,
$\left\{\begin{array}{l}{AB=AD}\\{AC=AC}\\{BC=DC}\end{array}\right.$
∴△ABC≌△ADC(SSS);
(2)∵△ABC≌△ADC,
∴∠BAC=∠DAC,
又∵AB=AD,
∴AC垂直平分BD.
点评 本题考查了全等三角形的性质和判定,等腰三角形的性质的应用,能求出△ABC≌△ADC是解此题的关键,注意:全等三角形的对应边相等,对应角相等.

练习册系列答案
相关题目
19.下列图形中,既是轴对称,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
3. 在△ABC中,AB=AC,BD为△ABC的高,如果∠BAC=40°,则∠CBD的度数是( )
在△ABC中,AB=AC,BD为△ABC的高,如果∠BAC=40°,则∠CBD的度数是( )
 在△ABC中,AB=AC,BD为△ABC的高,如果∠BAC=40°,则∠CBD的度数是( )
在△ABC中,AB=AC,BD为△ABC的高,如果∠BAC=40°,则∠CBD的度数是( )| A. | 70° | B. | 40° | C. | 20° | D. | 30° |
20.若x2-6x+9=16,则x=( )
| A. | 7 | B. | -1 | C. | 7或-1 | D. | 无法确定 |
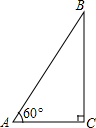 在Rt△ABC中,∠C=90°,∠A=60°,∠A,∠B,∠C的对边分别为a,b,c,a+b=3+$\sqrt{3}$,请你根据此条件,求斜边c的长.
在Rt△ABC中,∠C=90°,∠A=60°,∠A,∠B,∠C的对边分别为a,b,c,a+b=3+$\sqrt{3}$,请你根据此条件,求斜边c的长.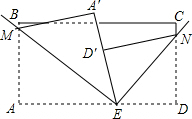 如图,长方形纸片ABCD,点E为AD边上的点,将纸片先沿直线EM对折,对折后的点A的对应点为A′,再沿直线EN对阵,对折后点D的对应点为D′,并且D′刚好落在A′E边上.
如图,长方形纸片ABCD,点E为AD边上的点,将纸片先沿直线EM对折,对折后的点A的对应点为A′,再沿直线EN对阵,对折后点D的对应点为D′,并且D′刚好落在A′E边上.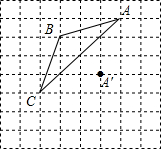 如图,正方形网格中每个小正方形的边长为1,格点△ABC的顶点A(1,2)、B(-2,1),将△ABC平移得到△A′B′C′,使得点A的对应点A′,试解答下列问题:
如图,正方形网格中每个小正方形的边长为1,格点△ABC的顶点A(1,2)、B(-2,1),将△ABC平移得到△A′B′C′,使得点A的对应点A′,试解答下列问题: