题目内容
13.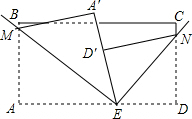 如图,长方形纸片ABCD,点E为AD边上的点,将纸片先沿直线EM对折,对折后的点A的对应点为A′,再沿直线EN对阵,对折后点D的对应点为D′,并且D′刚好落在A′E边上.
如图,长方形纸片ABCD,点E为AD边上的点,将纸片先沿直线EM对折,对折后的点A的对应点为A′,再沿直线EN对阵,对折后点D的对应点为D′,并且D′刚好落在A′E边上.(1)若∠AEM=40°,则∠A′EM=40°,∠DEN=50°;
(2)若∠AEM=n(0°<n<90°)猜想:∠MEN=90°,请你说明理由.
分析 (1)由折叠性质得∠AEM=∠A′EM,∠DEN=∠D′EN,即可得出结果;
(2)设∠AEN=∠A′EN=α,∠BEM=∠B′EM=β,得到2α+2β=180°,即可得出结论.
解答 解(1)由折叠性质得:∠AEM=∠A′EM,∠DEN=∠D′EN,
∴∠A′EM=40°,
∠DEN=$\frac{1}{2}$(180°-∠AEM-∠A′EM)=$\frac{1}{2}$(180°-40°-40°)=50°;
(2)∠MEN=90°,理由如下:
设∠AEN=∠A′EN=α,∠BEM=∠B′EM=β,
∴2α+2β=180°,
∴α+β=90°,
即∠MEN=90°.
故答案为:40,50,90.
点评 本题主要考查了翻折变换的性质及其应用问题;灵活运用翻折变换的性质来分析、判断、推理是解决问题的关键.

练习册系列答案
相关题目
4.下列各组数中,互为相反数的是( )
| A. | -(-5)和-5 | B. | 2和-$\frac{1}{2}$ | C. | -|-0.31|和0.3 | D. | -(+6)和+(-6) |
1.下列说法正确的是( )
| A. | 两个等边三角形一定全等 | B. | 面积相等的两个三角形全等 | ||
| C. | 形状相同的两个三角形全等 | D. | 全等三角形的面积一定相等 |
5. 如图所示,二次函数y=-x2+2x+k的图象与x轴的一个交点坐标为(3,0),则关于x的一元二次方程-x2+2x+k=0的解为( )
如图所示,二次函数y=-x2+2x+k的图象与x轴的一个交点坐标为(3,0),则关于x的一元二次方程-x2+2x+k=0的解为( )
 如图所示,二次函数y=-x2+2x+k的图象与x轴的一个交点坐标为(3,0),则关于x的一元二次方程-x2+2x+k=0的解为( )
如图所示,二次函数y=-x2+2x+k的图象与x轴的一个交点坐标为(3,0),则关于x的一元二次方程-x2+2x+k=0的解为( )| A. | x1=3,x2=-2 | B. | x1=3,x2=-1 | C. | x1=1,x2=-1 | D. | x1=3,x2=-3 |
3. 如图,△ABC≌△ADE,∠B=80°,∠C=30°,∠DAC=30°,则∠EAC的度数是( )
如图,△ABC≌△ADE,∠B=80°,∠C=30°,∠DAC=30°,则∠EAC的度数是( )
 如图,△ABC≌△ADE,∠B=80°,∠C=30°,∠DAC=30°,则∠EAC的度数是( )
如图,△ABC≌△ADE,∠B=80°,∠C=30°,∠DAC=30°,则∠EAC的度数是( )| A. | 35° | B. | 40° | C. | 25° | D. | 30° |
 如图,在△ABC中,AB=AC,点M在BC边上,ME⊥AB于点E,MF⊥AC于点F,且ME=MF.求证:MB=MC.
如图,在△ABC中,AB=AC,点M在BC边上,ME⊥AB于点E,MF⊥AC于点F,且ME=MF.求证:MB=MC. 如图,四边形ABCD的对角线AC与BD相交于点O,AB=AD,CB=CD.求证:
如图,四边形ABCD的对角线AC与BD相交于点O,AB=AD,CB=CD.求证: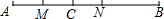 如图,线段AC=6,线段BC=9,点M是AC的中点,N在线段BC上,切$\frac{CN}{NB}$=$\frac{1}{2}$,则线段MN的长是( )
如图,线段AC=6,线段BC=9,点M是AC的中点,N在线段BC上,切$\frac{CN}{NB}$=$\frac{1}{2}$,则线段MN的长是( )