题目内容
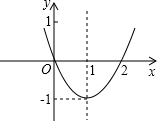 抛物线y=ax2+bx+c(a≠0)如图,回答:
抛物线y=ax2+bx+c(a≠0)如图,回答:(1)这个二次函数的表达式是
(2)当x=
(3)根据图象回答:当
考点:待定系数法求二次函数解析式,二次函数的性质
专题:
分析:(1)已知顶点坐标和函数图象经过原点,故设抛物线解析式为y=a(x-1)2-1(a≠0),然后把原点坐标代入来求a的值;
(2)把y=3代入(1)中函数关系进行解答相应的x的值;
(3)根据图示直接填空.
(2)把y=3代入(1)中函数关系进行解答相应的x的值;
(3)根据图示直接填空.
解答:解:(1)如图,抛物线的顶点坐标是(1,-1).
故设抛物线解析式为y=a(x-1)2-1(a≠0),
又∵抛物线经过点(0,0),
∴0=a(0-1)2-1,
解得,a=1.
故抛物线的解析式为:y=(x-1)2-1.
故填:y=(x-1)2-1;
(2)由(1)知,y=(x-1)2-1,
当y=3时,3=(x-1)2-1,
解得,x=3或x=-1.
故填:3或-1;
(3)根据图示知,当 x<0或x>2时,y>0.
故填:x<0或x>2.
故设抛物线解析式为y=a(x-1)2-1(a≠0),
又∵抛物线经过点(0,0),
∴0=a(0-1)2-1,
解得,a=1.
故抛物线的解析式为:y=(x-1)2-1.
故填:y=(x-1)2-1;
(2)由(1)知,y=(x-1)2-1,
当y=3时,3=(x-1)2-1,
解得,x=3或x=-1.
故填:3或-1;
(3)根据图示知,当 x<0或x>2时,y>0.
故填:x<0或x>2.
点评:本题考查了待定系数法求二次函数的解析式.
二次函数的解析式有三种常见形式:
①一般式:y=ax2+bx+c(a,b,c是常数,a≠0);
②顶点式:y=a(x-h)2+k(a,h,k是常数,a≠0),其中(h,k)为顶点坐标;
③交点式:y=a(x-x1)(x-x2)(a,b,c是常数,a≠0).
二次函数的解析式有三种常见形式:
①一般式:y=ax2+bx+c(a,b,c是常数,a≠0);
②顶点式:y=a(x-h)2+k(a,h,k是常数,a≠0),其中(h,k)为顶点坐标;
③交点式:y=a(x-x1)(x-x2)(a,b,c是常数,a≠0).

练习册系列答案
相关题目
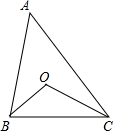 如图,在△ABC中,∠ABC=80°,∠ACB=60°,点O为内心,则∠BOC=
如图,在△ABC中,∠ABC=80°,∠ACB=60°,点O为内心,则∠BOC= 如图,在Rt△ABC中,∠C=90°,则:
如图,在Rt△ABC中,∠C=90°,则: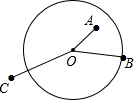 如图,设⊙O的半径为r,A点在圆内,OA
如图,设⊙O的半径为r,A点在圆内,OA 如图,直线l上有三个正方形a、b、c,若a、c的面积分别为5和11,则正方形b的边长为
如图,直线l上有三个正方形a、b、c,若a、c的面积分别为5和11,则正方形b的边长为 如图,平面内4条直线L1、L2、L3、L4是一组平行线,相邻2条平行线间的距离都是1个单位长度,正方形ABCD的4个顶点A、B、C、D都在这些平行线上,其中点A、C分别在直线L1和L4上,该正方形的面积是( )平方单位.
如图,平面内4条直线L1、L2、L3、L4是一组平行线,相邻2条平行线间的距离都是1个单位长度,正方形ABCD的4个顶点A、B、C、D都在这些平行线上,其中点A、C分别在直线L1和L4上,该正方形的面积是( )平方单位.