题目内容
在同一平面内,若∠BOA=80°,∠BOC=55°,OD是∠BOA的角平分线,则∠COD的度数为 .
考点:角平分线的定义
专题:
分析:分类讨论:OC在∠AOB外,OC在∠AOB内两种情况.根据角平分线的性质,可得∠BOD与∠AOB的关系,再根据角的和差,可得答案.
解答: 解:①OC在∠AOB外,如图1,
解:①OC在∠AOB外,如图1,
∵OD是∠AOB的平分线,∠AOB=80°,
∴∠B0D=
∠AOB=40°,
∠COD=∠B0D+∠BOC
=40°+55°
=95°;
②OC在∠AOB内,如图2,
∵OD是∠AOB的平分线,∠AOB=80°,
∴∠B0D=
∠AOB=40°,
∠COD=∠B0C-∠BOD,
=55°-40°,
=15°,
故答案为:95°或15°.
 解:①OC在∠AOB外,如图1,
解:①OC在∠AOB外,如图1,∵OD是∠AOB的平分线,∠AOB=80°,
∴∠B0D=
| 1 |
| 2 |
∠COD=∠B0D+∠BOC
=40°+55°
=95°;
②OC在∠AOB内,如图2,
∵OD是∠AOB的平分线,∠AOB=80°,
∴∠B0D=
| 1 |
| 2 |
∠COD=∠B0C-∠BOD,
=55°-40°,
=15°,
故答案为:95°或15°.
点评:本题主要考查了角的计算,关键是注意此题有两种情况,要进行讨论讨论,不要漏解.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
若△ABC≌△DEF,∠A=80°,∠B=40°,那么∠F的度数是( )
| A、80° | B、40° |
| C、60° | D、120° |

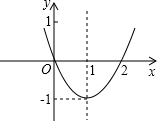 抛物线y=ax2+bx+c(a≠0)如图,回答:
抛物线y=ax2+bx+c(a≠0)如图,回答: