题目内容
 如图,在Rt△ABC中,∠C=90°,则:
如图,在Rt△ABC中,∠C=90°,则:(1)∠A的正切:tanA=
| ∠A的对边 |
| ∠A的邻边 |
(2)∠B的正切:tanB=
| ∠B的对边 |
| ∠B的邻边 |
(3)由(1)、(2)得:tanA•tanB=
考点:锐角三角函数的定义
专题:
分析:(1)(2)根据正切定义填空即可;
(3)利用(1)(2)中的线段比值进行计算可得答案.
(3)利用(1)(2)中的线段比值进行计算可得答案.
解答:解:(1)tanA=
=
;
(2)tanB=
=
;
(3)tanA•tanB=
•
=1.
故答案为:
;
;
;
;1.
| CB |
| AC |
| a |
| b |
(2)tanB=
| AC |
| CB |
| b |
| a |
(3)tanA•tanB=
| a |
| b |
| b |
| a |
故答案为:
| CB |
| AC |
| a |
| b |
| AC |
| CB |
| b |
| a |
点评:此题主要考查了正切定义,关键是掌握tanA=
.
| ∠A的对边 |
| ∠A的邻边 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若点P在第四象限,且距离每个坐标轴都是3个单位长度,则点P的坐标为( )
| A、(3,3) |
| B、(-3,3) |
| C、(3,-3) |
| D、(-3,-3) |
 如图,若∠A=70°,∠ABD=120°,则∠ACB=
如图,若∠A=70°,∠ABD=120°,则∠ACB= 如图,对于锐角A的每一个确定的值,sinA,cosA,tanA都有唯一确定的值与它对应,所以sinA,cosA,tanA都是A的
如图,对于锐角A的每一个确定的值,sinA,cosA,tanA都有唯一确定的值与它对应,所以sinA,cosA,tanA都是A的 央视节目主持人在主持节目时,站在舞台的黄金分割点处最自然得体.如图,若舞台AB长为20米,主持人至少应走到离A点
央视节目主持人在主持节目时,站在舞台的黄金分割点处最自然得体.如图,若舞台AB长为20米,主持人至少应走到离A点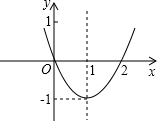 抛物线y=ax2+bx+c(a≠0)如图,回答:
抛物线y=ax2+bx+c(a≠0)如图,回答: