题目内容
15．已知a、b、c为△ABC的三边，且满足（a-b）（a2+b2-c2）=0，则△ABC是（ ）| A． | 等边三角形 | B． | 直角三角形 | ||
| C． | 等腰直角三角形 | D． | 等腰三角形或直角三角形 |
分析 由（a-b）（a2+b2-c2）=0，可得：a-b=0，或a2+b2-c2=0，进而可得a=b或a2+b2=c2，进而判断△ABC的形状为等腰三角形或直角三角形．
解答 解：∵（a-b）（a2+b2-c2）=0，
∴a-b=0，或a2+b2-c2=0，
即a=b或a2+b2=c2，
∴△ABC的形状为等腰三角形或直角三角形．
故选：D．
点评 此题考查了利用边判断三角形的形状，有两边相等的三角形是等腰三角形，满足a2+b2=c2的三角形是直角三角形．
练习册系列答案
相关题目
6．已知抛物线y=x2-2kx-1的对称轴在y轴右侧，则直线y=kx-3的图象经过的象限是（ ）
| A． | 第二、三、四象限 | B． | 第一、二、三象限 | C． | 第一、三、四象限 | D． | 第一、二、四象限 |
10．下列说法中正确的是（ ）
| A． | 相等的角是对顶角 | |
| B． | 同位角相等 | |
| C． | 如果两直线不相交，那么它们就平行 | |
| D． | 直线c外一点A与直线c上各点连接而成的所有线段中，最短线段的长是3cm，则点A到直线c的距离是3cm |
7．下列说法中，正确的是（ ）
| A． | 检测我市正在销售的酸奶的质量，应该采用抽样调查的方式 | |
| B． | 在连续5次数学周考测试中，两名同学的平均分相同，方差较大的同学数学成绩更稳定 | |
| C． | 某同学连续10次投掷质量均匀的硬币，3次正面向上，因此正面向上的概率是30% | |
| D． | “打开电视机，正在播放少儿节目”是必然事件 |
5．
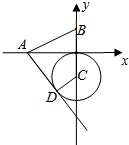如图，已知A，B两点的坐标分别为（-2，0），（0，1），⊙C的圆心坐标为（0，-1），半径为1，射线AD切⊙C于D，则四边形ABCD面积的是（ ）
如图，已知A，B两点的坐标分别为（-2，0），（0，1），⊙C的圆心坐标为（0，-1），半径为1，射线AD切⊙C于D，则四边形ABCD面积的是（ ）| A． | $\sqrt{5}$+1 | B． | 6 | C． | 4 | D． | 3 |