题目内容
3.已知a,b 是方程x2-x-2=0的两个不相等实数根,则a+b-ab的值是3.分析 由a,b是方程x2-x-2=0的两个不相等的实数根,利用根与系数的关系即可求出两根之和和两根之积,代入代数式即可求解.
解答 解:∵a,b是方程x2-x-2=0的两个不相等的实数根,
∴a+b=1,ab=-2.
∴a+b-ab=1-(-2)=3,
故答案为:3.
点评 此题考查了根与系数的关系,一元二次方程ax2+bx+c=0(a≠0),当方程有解,即b2-4ac≥0时,设方程的解分别为x1,x2,则有x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
13.若|x-5|+2$\sqrt{y+2}$=0,则x-y的值是( )
| A. | -7 | B. | -5 | C. | 3 | D. | 7 |
15.已知a、b、c为△ABC的三边,且满足(a-b)(a2+b2-c2)=0,则△ABC是( )
| A. | 等边三角形 | B. | 直角三角形 | ||
| C. | 等腰直角三角形 | D. | 等腰三角形或直角三角形 |
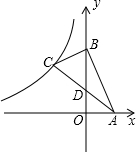 如图所示,直线y=-3x+6交x轴、y轴于A、B两点,BC⊥AB,且D为AC的中点,双曲线y=$\frac{k}{x}$过点C,则k=-$\frac{32}{3}$.
如图所示,直线y=-3x+6交x轴、y轴于A、B两点,BC⊥AB,且D为AC的中点,双曲线y=$\frac{k}{x}$过点C,则k=-$\frac{32}{3}$.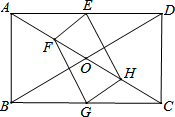 已知,在矩形ABCD中,对角线AC、BD相交于点O,E、F、G、H分别是AD、OA、BC、OC的中点.
已知,在矩形ABCD中,对角线AC、BD相交于点O,E、F、G、H分别是AD、OA、BC、OC的中点.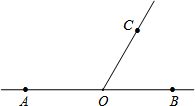 已知:如图,点O是直线AB上一点,过点O作射线OC,使∠AOC=120°.
已知:如图,点O是直线AB上一点,过点O作射线OC,使∠AOC=120°.