题目内容
5.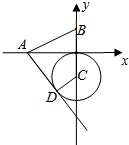 如图,已知A,B两点的坐标分别为(-2,0),(0,1),⊙C的圆心坐标为(0,-1),半径为1,射线AD切⊙C于D,则四边形ABCD面积的是( )
如图,已知A,B两点的坐标分别为(-2,0),(0,1),⊙C的圆心坐标为(0,-1),半径为1,射线AD切⊙C于D,则四边形ABCD面积的是( )| A. | $\sqrt{5}$+1 | B. | 6 | C. | 4 | D. | 3 |
分析 设EF=x,由切割线定理表示出DE,可证明△CDE∽△AOE,根据相似三角形的性质可求得x,然后求得△ABE面积.再求得△CDE面积,进而可求出四边形ABCD面积.
解答 解:由题意可知:当射线AD与⊙C相切时,△ABE面积的最大.
连接AC,
∵∠AOC=∠ADC=90°,AC=AC,OC=CD,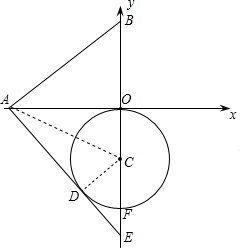
∴Rt△AOC≌Rt△ADC,
∴AD=AO=2,
连接CD,设EF=x,
∴DE2=EF•OE,
∵CF=1,
∴DE=$\sqrt{x(x+2)}$,
∴△CDE∽△AOE,
∴$\frac{CD}{AO}=\frac{CE}{AE}$,
即$\frac{1}{2}=\frac{x+1}{2+\sqrt{x(x+2)}}$,
解得x=$\frac{2}{3}$,
S△ABE=$\frac{BE•AO}{2}$=$\frac{11}{3}$,
∵S△CDE=$\frac{1}{2}$DE•CD=$\frac{1}{2}$×$\frac{4}{3}$×1=$\frac{2}{3}$,
∴四边形ABCD面积的=$\frac{11}{3}$-$\frac{2}{3}$=3,
故选:D.
点评 本题是一个动点问题,考查了圆的综合题,解题时,涉及到了切线的性质和三角形面积的计算,解题的关键是求出△ABE面积和△CDE面积,题目的难度较大.

练习册系列答案
相关题目
15.已知a、b、c为△ABC的三边,且满足(a-b)(a2+b2-c2)=0,则△ABC是( )
| A. | 等边三角形 | B. | 直角三角形 | ||
| C. | 等腰直角三角形 | D. | 等腰三角形或直角三角形 |
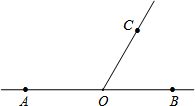 已知:如图,点O是直线AB上一点,过点O作射线OC,使∠AOC=120°.
已知:如图,点O是直线AB上一点,过点O作射线OC,使∠AOC=120°.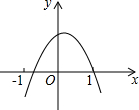 如图,抛物线y=ax2+bx+c的开口向下,交x轴的正半轴(1,0),则下列结论:(1)-abc<0;(2)a-b+c<0(3)2a+b<0;(4)a+c<0,正确的序数有(2)(3)(4).
如图,抛物线y=ax2+bx+c的开口向下,交x轴的正半轴(1,0),则下列结论:(1)-abc<0;(2)a-b+c<0(3)2a+b<0;(4)a+c<0,正确的序数有(2)(3)(4).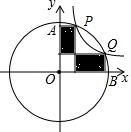 如图,点P(2,6)是函数y=$\frac{k}{x}$(k≠0)图象上的一点,以OP为半径作扇形OAB,交y轴于点A,交x轴于点B,且与函数y=$\frac{k}{x}$(k≠0)图象交于点Q.从点P,Q分别向x轴,y轴作垂线,则图中阴影部分的面积是16.
如图,点P(2,6)是函数y=$\frac{k}{x}$(k≠0)图象上的一点,以OP为半径作扇形OAB,交y轴于点A,交x轴于点B,且与函数y=$\frac{k}{x}$(k≠0)图象交于点Q.从点P,Q分别向x轴,y轴作垂线,则图中阴影部分的面积是16.