题目内容

4．解不等式组：$\left\{\begin{array}{l}{x-3（x-2）≥4}\\{\frac{1+2x}{3}＜x+1}\end{array}\right.$，并把解集在下面数轴上表示出来．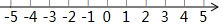

分析 先求出不等式的解集，再求出不等式组的解集即可．

解答 解：$\left\{\begin{array}{l}{x-3（x-2）≥4①}\\{\frac{1+2x}{3}＜x+1②}\end{array}\right.$
∵解不等式①得：x≤1，
解不等式②得：x＞-2，
∴不等式组的解集为-2＜x≤1，
在数轴上表示为：．

点评 本题考查了解一元一次不等式组和在数轴上表示不等式组的解集，能根据不等式的解集求出不等式组的解集是解此题的关键．

练习册系列答案
相关题目
14．在平面直角坐标系中，点A的坐标为（3，0），点B的坐标为（-1，0），点C在y轴上，如果三角形ABC的面积等于6，那么点C的坐标为（0，3）或（0，-3）．
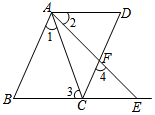15．完成下面推理步骤，并在每步后面的括号内填写出推理根据：
如图，已知AB∥CD，∠1=∠2，∠3=∠4，试说明AD∥BE．
解：∵AB∥CD（已知），
∴∠4=∠BAE（两直线平行，同位角相等），
∵∠3=∠4（已知）
∴∠3=∠BAE（等量代换），
∵∠1=∠2（已知），
∴∠CAE+∠1=∠CAE+∠2，
即∠BAE=∠DAC，
∴∠3=∠DAC，
∴AD∥BE（内错角相等，两直线平行）．
12．科技小组进行了机器人行走性能试验，如图1，甲，乙两机器人分别从M，N两点同时同向出发，经过7分钟，甲，乙同时到达P点，乙机器人始终以60米/分的速度行走，图2是甲，乙两机器人之间的距离y（米）与他们的行走时间x（分钟）之间的函数图象，请结合图形，回答下列问题：
（1）M，N两点之间的距离是70米，甲前2分钟的速度为95米/分；
（2）若前3分钟甲的速度不变，图2中，点F的坐标为（3，35）；
（3）若线段FG∥x轴，则此段时间内甲的速度为60米/分；
（4）求M，P两点之间的距离（写出解答过程）．
19．我国古代数学家赵爽的“勾股圆方图”是由四个全等的直角三角形与中间的一个小正方形拼成一个大正方形（如图所示），如果大正方形的面积是49，小正方形的面积为4，直角三角形的两直角边长分别为a，b，那么下列结论：
（1）a2+b2=49，（2）b-a=2，（3）ab=$\frac{45}{2}$，（4）a+b=$\sqrt{94}$中，
正确结论的个数有（　　）
A．4个B．3个C．2个D．1个
9．在△ABC中，AB=AC，AB的垂直平分线交AC于点N，交BC的延长线于点M，∠A=40°．
（1）求∠NMB的大小．
（2）如果将（1）中的∠A的度数改为70°，其余条件不变，再求∠NMB的大小．
（3）你认为存在什么样的规律？试用一句话说明．（请同学们自己画图）
（4）将（1）中的∠A改为钝角，对这个问题规律的认识是否需要加以修改？
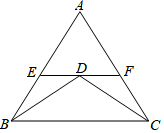16．填空：把下面的推理过程补充完整，并在括号内注明理由．
已知：EF∥BC，BD=CD，ED=FD，请说明BE=CF
解：∵BD=CD（已知）∴∠DBC=∠DCB （等边对等角）
∵EF∥BC（已知）
∴∠EDB=∠DBC；∠FDC=∠DCB（两直线平行内错角相等）
∴∠EDB=∠FDC（等量代换）
在△EBD和△FCD中，
ED=FD
∠EDB=∠FDC
BD=CD
∴△EBD≌△FCD（SAS）
∴BE=CF（全等三角形的对应边相等）
13．解方程 
（1）$\frac{x}{2}$-$\frac{x-1}{3}$=1
（2）x-$\frac{x-2}{5}$=$\frac{2x-5}{3}$-3．
14．实数n、m是连续整数，如果n＜$\sqrt{17}$＜m，那么m+n的值为（　　）
A．9B．10C．11D．12

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网