题目内容
9.在△ABC中,AB=AC,AB的垂直平分线交AC于点N,交BC的延长线于点M,∠A=40°.(1)求∠NMB的大小.
(2)如果将(1)中的∠A的度数改为70°,其余条件不变,再求∠NMB的大小.
(3)你认为存在什么样的规律?试用一句话说明.(请同学们自己画图)
(4)将(1)中的∠A改为钝角,对这个问题规律的认识是否需要加以修改?
分析 (1)由在△ABC中,AB=AC,∠A=40°,根据等腰三角形的性质,可求得∠ABC的度数,又由AB的垂直平分线交AC于点N,交BC的延长线于点M,即可求得答案;
(2)由在△ABC中,AB=AC,∠A=70°,根据等腰三角形的性质,可求得∠ABC的度数,又由AB的垂直平分线交AC于点N,交BC的延长线于点M,即可求得答案;
(3)由在△ABC中,AB=AC,根据等腰三角形的性质,即可用∠A表示出∠ABC,又由AB的垂直平分线交AC于点N,交BC的延长线于点M,即可求得答案.
(4)由以上证明方法可得答案.
解答 解:(1)∵在△ABC中,AB=AC,∠A=40°,
∴∠ABC=∠ACB=70°,
∵AB的垂直平分线交AC于点N,交BC的延长线于点M,
∴MN⊥AB,
∴∠NMB=90°-∠ABC=20°;
(2)∵在△ABC中,AB=AC,∠A=70°,
∴∠ABC=∠ACB=55°,
∵AB的垂直平分线交AC于点N,交BC的延长线于点M,
∴MN⊥AB,
∴∠NMB=90°-∠ABC=35°;
(3)等腰三角形一腰上的中垂线与底边延长线所成夹角度数是顶角的一半,即∠NMB=$\frac{1}{2}$∠A.
理由:如图,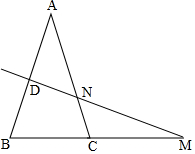
∵在△ABC中,AB=AC,
∴∠ABC=∠ACB=$\frac{180°-∠A}{2}$,
∵AB的垂直平分线交AC于点N,交BC的延长线于点M,
∴MN⊥AB,
∴∠NMB=90°-∠ABC=$\frac{1}{2}$∠A.
(4)如图2,将(1)中的∠A改为钝角,(3)中猜想的结论结论仍然成立,不需要修改.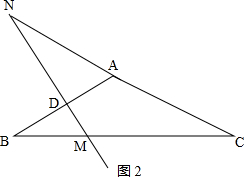
∵在△ABC中,AB=AC,
∴∠ABC=∠ACB=$\frac{180°-∠A}{2}$,
∵AB的垂直平分线交直线AC于点N,交BC于点M,
∴MN⊥AB,
∴∠NMB=90°-∠ABC=$\frac{1}{2}$∠A.
点评 此题考查了线段垂直平分线的性质以及等腰三角形的性质.此题难度不大,注意掌握数形结合思想的应用.

 阅读快车系列答案
阅读快车系列答案
| A. | A→B→C→A | B. | A→B→C→D | C. | A→D→O→A | D. | A→O→B→C |
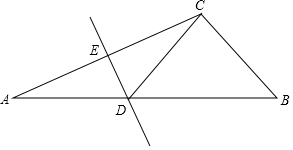 如图,在△ABC中,∠ACB=111°,AC边上的垂直平分线交AB于点D,交AC边于点E,连接CD.
如图,在△ABC中,∠ACB=111°,AC边上的垂直平分线交AB于点D,交AC边于点E,连接CD.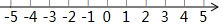
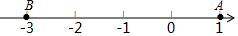 如图,已知数轴上两点A,B对应的数分别为1,-3,点P为数轴上一动点,点P以每秒0.5个单位的速度从O点向左运动,则经过4或10秒,使PA=3PB.
如图,已知数轴上两点A,B对应的数分别为1,-3,点P为数轴上一动点,点P以每秒0.5个单位的速度从O点向左运动,则经过4或10秒,使PA=3PB.