题目内容
15. 完成下面推理步骤,并在每步后面的括号内填写出推理根据:
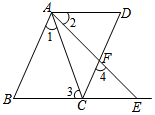
完成下面推理步骤,并在每步后面的括号内填写出推理根据:如图,已知AB∥CD,∠1=∠2,∠3=∠4,试说明AD∥BE.
解:∵AB∥CD(已知),
∴∠4=∠BAE(两直线平行,同位角相等),
∵∠3=∠4(已知)
∴∠3=∠BAE(等量代换),
∵∠1=∠2(已知),
∴∠CAE+∠1=∠CAE+∠2,
即∠BAE=∠DAC,
∴∠3=∠DAC,
∴AD∥BE(内错角相等,两直线平行).
分析 首先由平行线的性质可得∠4=∠BAE,然后结合已知,通过等量代换推出∠3=∠DAC,最后由内错角相等,两直线平行可得AD∥BE.
解答 解:∵AB∥CD(已知),
∴∠4=∠BAE(两直线平行,同位角相等),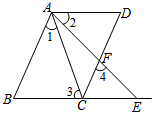 ∵∠3=∠4(已知)
∵∠3=∠4(已知)
∴∠3=∠BAE(等量代换),
∵∠1=∠2(已知),
∴∠CAE+∠1=∠CAE+∠2,
即∠BAE=∠DAC,
∴∠3=∠DAC,
∴AD∥BE(内错角相等,两直线平行).
故答案为:BAE;两直线平行,同位角相等;BAE;等量代换;1;2;BAE;DAC;DAC;内错角相等,两直线平行.
点评 本题主要考查平行线的性质和性质,掌握平行线的性质和判定是解题的关键,即①两直线平行?同位角相等,②两直线平行?内错角相等,③两直线平行?同旁内角互补,④a∥b,b∥c⇒a∥c.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
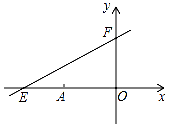 如图,直线y=kx+6与x、y轴分别交于E、F.点E坐标为(-8,0),点A的坐标为(-6,0),P(x,y)是直线y=kx+6上的一个动点.
如图,直线y=kx+6与x、y轴分别交于E、F.点E坐标为(-8,0),点A的坐标为(-6,0),P(x,y)是直线y=kx+6上的一个动点.
 如图是一个数表,现用一个矩形在数表中任意框出4个数,则
如图是一个数表,现用一个矩形在数表中任意框出4个数,则