题目内容
2．
如图，直线y1=x+b与y2=kx-1相交于点P，则关于x的不等式x+b＞kx-1的解集为x＞-1．
分析 观察函数图象得到，当x＞-1，函数y=x+b的图象都在函数y=kx-1图象的上方，于是可得到关于x的不等式x+b＞kx-1的解集．
解答 解：当x＞-1，函数y=x+b的图象在函数y=kx-1图象的上方，
所以关于x的不等式x+b＞kx-1的解集为x＞-1．
故答案为x＞-1．
点评 本题考查了一次函数与一元一次不等式：从函数的角度看，就是寻求使一次函数y=ax+b的值大于（或小于）0的自变量x的取值范围；从函数图象的角度看，就是确定直线y=kx+b在x轴上（或下）方部分所有的点的横坐标所构成的集合．
练习册系列答案
相关题目
12．
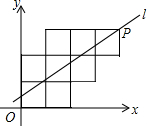八个边长为1的正方形如图摆放在平面直角坐标系中，经过P点的一条直线l将这八个正方形分成面积相等的两部分，则该直线l的解析式为（ ）
八个边长为1的正方形如图摆放在平面直角坐标系中，经过P点的一条直线l将这八个正方形分成面积相等的两部分，则该直线l的解析式为（ ）| A． | $y=\frac{2}{3}x+\frac{1}{3}$ | B． | y=$\frac{5}{8}$x+$\frac{1}{2}$ | C． | $y=\frac{7}{12}x+\frac{2}{3}$ | D． | $y=\frac{9}{16}x+\frac{3}{4}$ |
13．如果A（2，y1），B（3，y2）两点都在反比例函数y=$\frac{1}{x}$的图象上，那么y1与y2的大小关系是（ ）
| A． | y1＜y2 | B． | y1＞y2 | C． | y1=y2 | D． | y1≥y2 |
小王同学的家和学校在一条笔直的马路旁，某天小丽沿着这条马路上学，先从家步行到公交站台甲，再乘车到公交站如乙下车，最后步行到学校（在整个过程中小丽步行的速度不变）．图中折线ABCDE表示小丽和学校之间的距离y（米）与她离家时间x（分钟）之间的函数关系．
如图，已知在△ABC中，∠1=∠2，∠3=∠4，∠BAC=84°．求∠DAC的度数．
20．从二次根式$\sqrt{12}$、$\sqrt{{x}^{2}+3}$、$\sqrt{\frac{3}{2}}$、$\sqrt{{a}^{2}b}$、2$\sqrt{0.5}$、$\sqrt{26}$中任选一个，不是最简二次根式的概率是（ ）
| A． | $\frac{1}{6}$ | B． | $\frac{2}{3}$ | C． | $\frac{1}{3}$ | D． | $\frac{1}{2}$ |