题目内容
9.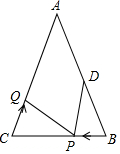 如图,已知△ABC中,∠B=∠C,AB=8厘米,BC=6厘米,点D为AB的中点,如果点P在线段BC上以每秒2厘米的速度由B点向C点运动,同时,点Q在线段CA上以每秒a厘米的速度由C点向A点运动,设运动时间为t(秒)(0≤t<3).
如图,已知△ABC中,∠B=∠C,AB=8厘米,BC=6厘米,点D为AB的中点,如果点P在线段BC上以每秒2厘米的速度由B点向C点运动,同时,点Q在线段CA上以每秒a厘米的速度由C点向A点运动,设运动时间为t(秒)(0≤t<3).(1)用含t的代数式表示PC的长度:PC=6-2t.
(2)若点P、Q的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由;
(3)若点P、Q的运动速度不相等,当点Q的运动速度a为多少时,能够使△BPD与△CQP全等?
分析 (1)直接根据时间和速度表示PC的长;
(2)根据SAS证明△CQP≌△BPD即可;
(3)因为点P、Q的运动速度不相等,所以PB≠CQ,那么PB只能与PC相等,则PB=PC=3,CQ=BD=4,得2t=3,at=4,解出即可.
解答 解:(1)由题意得:PB=2t,
则PC=6-2t;
故答案为:6-2t;
(2,理由是:
当t=a=1时,PB=CQ=2,
∴PC=6-2=4,
∵∠B=∠C,
∴AC=AB=8,
∵D是AB的中点,
∴BD=$\frac{1}{2}$AB=4,
∴BD=PC=4,
在△CQP和△BPD中,
∵$\left\{\begin{array}{l}{PC=BD}\\{∠C=∠B}\\{CQ=PB}\end{array}\right.$,
∴△CQP≌△BPD(SAS);
(3)∵点P、Q的运动速度不相等,
∴PB≠CQ,
当△BPD于△CQP全等,且∠B=∠C,
∴BP=PC=3,CQ=BD=4,
∵BP=2t=3,CQ=at=4,
∴t=$\frac{3}{2}$,
∴$\frac{3}{2}$a=4,
a=$\frac{8}{3}$,
∴当a=$\frac{8}{3}$时,能够使△BPD与△CQP全等.
点评 本题是三角形的动点运动问题,考查了全等三角形的判定,主要运用了路程=速度×时间的公式,要求熟练运用全等三角形的判定和性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.下列关系中,两个量之间为反比例函数关系的是( )
| A. | 正方形的面积S与边长a的关系 | |
| B. | 正方形的周长L与边长a的关系 | |
| C. | 长方形的长为a,宽为20,其面积S与a的关系 | |
| D. | 长方形的面积为40,长为a,宽为b,a与b的关系 |
14.某商品在元旦假日准备开展促销活动,商品的标价为1000元,4折销售后任可赚80元,则该商品的成本价为( )
| A. | 400元 | B. | 440元 | C. | 320元 | D. | 270元 |
 如图,△ABC≌△ADE,若∠BAE=120°,∠BAD=40°,∠D=60°,则∠C的度数为40°.
如图,△ABC≌△ADE,若∠BAE=120°,∠BAD=40°,∠D=60°,则∠C的度数为40°.