题目内容
3.我们学习了勾股定理后,都知道“勾三、股四、弦五”.观察:3、4、5;5、12、13;7、24、25;9、40、41;…,发现这些勾股数的勾都是奇数,且从3起就没有间断过.
(1)请你根据上述的规律写出下两组勾股数:11、60,61; 13、84,85;
(2)若第一个数用字母a(a为奇数,且a≥3)表示,那么后两个数用含a的代数式分别表示为$\frac{{a}^{2}-1}{2}$和$\frac{{a}^{2}+1}{2}$,请用所学知识说明它们是一组勾股数.
分析 (1)分析所给四组的勾股数:3、4、5;5、12、13;7、24、25;9、40、41;可得下一组一组勾股数:11,60,61,进而得出答案;
(2)根据所提供的例子发现股是勾的平方减去1的二分之一,弦是勾的平方加1的二分之一.
解答 解:(1)∵3、4、5;5、12、13;7、24、25;9、40、41;…,
∴4=$\frac{{3}^{2}-1}{2}$,12=$\frac{{5}^{2}-1}{2}$,24=$\frac{{7}^{2}-1}{2}$…
∴11,60,61;13,84,85;
故答案为:60,61;84,85;
(2)后两个数表示为$\frac{{a}^{2}-1}{2}$和$\frac{{a}^{2}+1}{2}$,
∵a2+($\frac{{a}^{2}-1}{2}$)2=a2+$\frac{{a}^{4}-2{a}^{2}+1}{4}$=$\frac{{a}^{4}+2{a}^{2}+1}{4}$=$(\frac{{a}^{2}+1}{2})^{2}$,
$(\frac{{a}^{2}+1}{2})^{2}$=$\frac{{a}^{4}+2{a}^{2}+1}{4}$,
∴a2+($\frac{{a}^{2}-1}{2}$)2=$(\frac{{a}^{2}+1}{2})^{2}$,
又∵a≥3,且a为奇数,
∴由a,$\frac{{a}^{2}-1}{2}$,$\frac{{a}^{2}+1}{2}$三个数组成的数是勾股数.
故答案为:$\frac{{a}^{2}-1}{2}$,$\frac{{a}^{2}+1}{2}$.
点评 本题考查的是勾股数之间的关系,根据题目中所给的勾股数及关系式进行猜想、证明即可.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.式子|x-1|+3取最小值时,x等于( )
| A. | 1 | B. | 2 | C. | 3 | D. | 0 |
11.下列图形中,是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
15.2008年8月8日北京奥运会开幕式在国家体育场“鸟巢”举行.“鸟巢”建筑面积为2580000000cm2,数字2580000000用科学记数法表示为( )
| A. | 258×107 | B. | 25.8×108 | C. | 2.58×109 | D. | 2.58×1010 |
12.若k是方程3x+1=7的解,则4k+3的值是( )
| A. | 11 | B. | -11 | C. | 17 | D. | -7 |
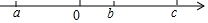 有理数a、b、c在数轴上的位置如图:化简:|b-c|+2|a+b|-|c-a|
有理数a、b、c在数轴上的位置如图:化简:|b-c|+2|a+b|-|c-a|