题目内容
11.在正方形ABCD中,点E,F,G分别是边AD,AB,BC的中点,点H是直线BC上一点.将线段FH绕点F逆时针旋转90°,得到线段FK,连接EK.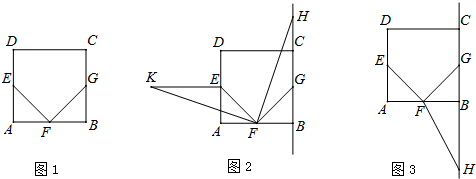
(1)如图1,求证:EF=FG,且EF⊥FG;
(2)如图2,若点H在线段BC的延长线上,猜想线段BH,EF,EK之间满足的数量关系,并证明你的结论.
(3)若点H在线段BC的反向延长线上,请在图3中补全图形并直接写出线段BH,EF,EK之间满足的数量关系.
分析 (1)根据正方形的性质证明△AEF≌△BGF,得到EF=FG,∠AFE=∠BFG=45°,根据三角形的内角和求得∠EFG=180°-∠AFE-∠BFG=90°,即EF⊥FG.
(2)BH=$\frac{{\sqrt{2}}}{2}$EF+EK;根据将线段FH绕点F逆时针旋转90°,得到线段FK,得到FH=FK,∠HFK=90°,所以∠KFE+∠EFH=90°,由∠EFG=90°,所以∠HFG+∠EFH=90°,得到∠KFE=∠HFG,证明△EFK≌△GFH,所以EK=GH.由△BFG是等腰直角三角形,所以BG=$\frac{{\sqrt{2}}}{2}$FG,得到BH=BG+GH=$\frac{{\sqrt{2}}}{2}$FG+EK=$\frac{{\sqrt{2}}}{2}$EF+EK,即BH=$\frac{{\sqrt{2}}}{2}$EF+EK.
(3)根据题意画出图形,然后根据(2)的方法直接得到结论.
解答 解:(1)∵正方形ABCD,E,F,G分别是边AD,AB,BC的中点,
∴AE=AF=FB=BG,∠A=∠B=90°,
在△AEF和△BGF中,
$\left\{\begin{array}{l}{AE=BG}\\{∠A=∠B}\\{AF=BF}\end{array}\right.$,
∴△AEF≌△BGF,
∴EF=FG,∠AFE=∠BFG=45°,
∴∠EFG=180°-∠AFE-∠BFG=90°,即EF⊥FG.
(2)BH=$\frac{{\sqrt{2}}}{2}$EF+EK;
证明:将线段FH绕点F逆时针旋转90°,得到线段FK,
∴FH=FK,∠HFK=90°,
∴∠KFE+∠EFH=90°,
∵∠EFG=90°,
∴∠HFG+∠EFH=90°,
∴∠KFE=∠HFG,
在△EFK和△GFH中,
$\left\{\begin{array}{l}{FK=FH}\\{∠KFE=∠HFG}\\{EF=FG}\end{array}\right.$,
∴△EFK≌△GFH,
∴EK=GH.
∵△BFG是等腰直角三角形,
∴BG=$\frac{{\sqrt{2}}}{2}$FG,
∴BH=BG+GH=$\frac{{\sqrt{2}}}{2}$FG+EK=$\frac{{\sqrt{2}}}{2}$EF+EK,
即BH=$\frac{{\sqrt{2}}}{2}$EF+EK.
(3)补全图形如图3: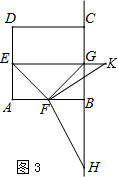
BH=EK-$\frac{{\sqrt{2}}}{2}$EF.
点评 本题考查了全等三角形的性质与判定,等腰直角三角形的性质,解决本题的关键是利用全等三角形的判定和等腰三角形的性质.

| A. | $\frac{x}{x+1}$ | B. | $\frac{1}{x-1}$ | C. | $\frac{{x}^{2}+1}{{x}^{2}}$ | D. | $\frac{{x}^{2}}{{x}^{2}+1}$ |
 如图,一个空心圆柱体,其左视图正确的是( )
如图,一个空心圆柱体,其左视图正确的是( )| A. |  | B. |  | C. |  | D. |  |
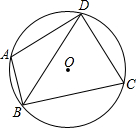 如图,⊙O过四边形ABCD的四个顶点,已知∠ABC=90°,BD平分∠ABC,则:①AD=CD,②$\sqrt{3}$BD=AB+CB,③点O是∠ADC平分线上的点,④AB2+BC2=2CD2,上述结论中正确的个数为( )
如图,⊙O过四边形ABCD的四个顶点,已知∠ABC=90°,BD平分∠ABC,则:①AD=CD,②$\sqrt{3}$BD=AB+CB,③点O是∠ADC平分线上的点,④AB2+BC2=2CD2,上述结论中正确的个数为( )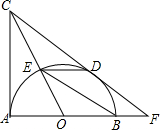 如图,AB为⊙O的直径,CA,CD为⊙O的切线.
如图,AB为⊙O的直径,CA,CD为⊙O的切线.