题目内容
1.计算$\frac{{{{2010}^3}-{{1000}^3}-{{1010}^3}}}{2010×1000×1010}$=3.分析 把分子的前两项用立方差分解因式,再利用提公式因法,整理可计算出分式的值为1010×2010×3000,再约分可求得其值.
解答 解:∵20103-10003-10103
=(20103-10003)-10103
=(2010-1000)(20102+2010×1000+10002)-10103
=1010×(20102+2010×1000+10002)-10103
=1010×[20102+2010×1000+(10002-10103)]
=1010×[20102+2010×1000+(1000+1010)(1000-1010)]
=1010×[20102+2010×1000-10×2010]
=1010×2010(2010+1000-10)
=1010×2010×3000,
∴$\frac{{{{2010}^3}-{{1000}^3}-{{1010}^3}}}{2010×1000×1010}$=$\frac{1010×2010×3000}{2010×1000×1010}$=3,
故答案为:3.
点评 本题主要考查因式分解的应用,掌握因式分解的方法是解题的关键,注意公式法、提公因式法、分组分解法的灵活运用.

练习册系列答案
相关题目
12.一根铁丝正好可以围成一个长是(2a+3b),宽是(a+b)的长方形框,把从这个长方形框上剪去的一段铁丝围成一个长是a,宽是b的长方形框(均不计接缝),则剩下的铁丝长是( )
| A. | a+2b | B. | b+2a | C. | 4a+6b | D. | 6a+4b |
11.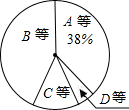 某校为了解九年级男生1000米长跑的成绩,从中随机抽取了50名男生进行测试,根据测试评分标准,将他们的得分进行统计后分为A,B,C,D四等,并绘制成下面的频数分布表和扇形统计图.
某校为了解九年级男生1000米长跑的成绩,从中随机抽取了50名男生进行测试,根据测试评分标准,将他们的得分进行统计后分为A,B,C,D四等,并绘制成下面的频数分布表和扇形统计图.
(1)试直接写出x=12,y=0.02;
(2)求C等的扇形的圆心角的度数;
(3)如果该校九年级共有男生200名,试估计这200名男生中成绩达到A等和B等的人数共有多少人?
 某校为了解九年级男生1000米长跑的成绩,从中随机抽取了50名男生进行测试,根据测试评分标准,将他们的得分进行统计后分为A,B,C,D四等,并绘制成下面的频数分布表和扇形统计图.
某校为了解九年级男生1000米长跑的成绩,从中随机抽取了50名男生进行测试,根据测试评分标准,将他们的得分进行统计后分为A,B,C,D四等,并绘制成下面的频数分布表和扇形统计图.| 等第 | 成绩(得分) | 频数(人数) | 频率 |
| A | 10分 | 7 | 0.14 |
| 9分 | x | ||
| B | 8分 | 15 | 0.30 |
| 7分 | 8 | 0.16 | |
| C | 6分 | 4 | 0.08 |
| 5分 | y | ||
| D | 5分以下 | 3 | 0.06 |
| 合计 | 50 | 1.00 |
(2)求C等的扇形的圆心角的度数;
(3)如果该校九年级共有男生200名,试估计这200名男生中成绩达到A等和B等的人数共有多少人?
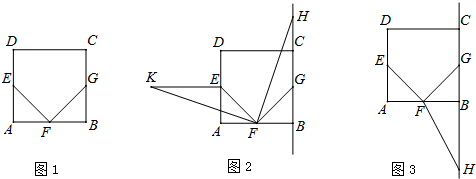
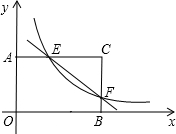 已知:在矩形AOBC中,OB=4,OA=3.分别以OB,OA所在直线为x轴和y轴,建立如图所示的平面直角坐标系.F是边BC上的一个动点(不与B,C重合),过F点的反比例函数y=$\frac{k}{x}$(k>0)的图象与AC边交于点E.
已知:在矩形AOBC中,OB=4,OA=3.分别以OB,OA所在直线为x轴和y轴,建立如图所示的平面直角坐标系.F是边BC上的一个动点(不与B,C重合),过F点的反比例函数y=$\frac{k}{x}$(k>0)的图象与AC边交于点E.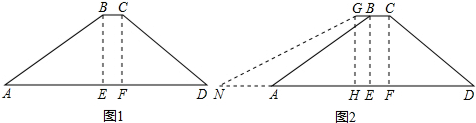
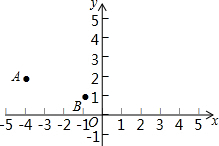 如图,A(-4,2),B(-1,1),在x轴上找一点P,使|PA-PB|的值最大,求点P的坐标.
如图,A(-4,2),B(-1,1),在x轴上找一点P,使|PA-PB|的值最大,求点P的坐标. 如图,?ABCD的一边AB为直径的⊙O过点C,连结OC,若∠AOC=80°,则∠BCD=140度.
如图,?ABCD的一边AB为直径的⊙O过点C,连结OC,若∠AOC=80°,则∠BCD=140度.