题目内容
11.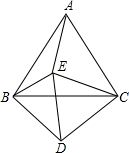 如图,△ABC和△CDE都是等边三角形,且∠EBD=66°,则∠AEB的大小=126°.
如图,△ABC和△CDE都是等边三角形,且∠EBD=66°,则∠AEB的大小=126°.
分析 由等边三角形的性质得出BC=AC,∠ABC=∠ACB=∠BAC=∠DCE=60°,CD=CE,得出∠BCD=∠ACE,由SAS证明△BCD≌△ACE,得出∠CBD=∠CAE,再证明∠CBD-6°=∠ABE,得出∠ABE=∠CAE-6°,求出∠ABE+∠BAE=∠BAC-6°,即可求出∠AEB的大小.
解答 解:∵△ABC和△CDE都是等边三角形,
∴BC=AC,∠ABC=∠ACB=∠BAC=∠DCE=60°,CD=CE,
∴∠BCD=∠ACE,
在△BCD和△ACE中,$\left\{\begin{array}{l}{BC=AC}&{\;}\\{∠BCD=∠ACE}&{\;}\\{CD=CE}&{\;}\end{array}\right.$,
∴△BCD≌△ACE(SAS),
∴∠CBD=∠CAE,
∵∠EBD=66°,
∴∠CBD=∠ABE+(66°-60°)
∴∠ABE=∠CAE-6°,
∵∠ABE+∠BAE=∠CAE+∠BAE-6°=∠BAC-6°=54°,
∴∠AEB=180°-54°=126°;
故答案为:126°.
点评 本题考查了等边三角形的性质、全等三角形的判定与性质;熟练掌握等边三角形的性质,证明三角形全等得出对应角相等是解决问题的关键.

练习册系列答案
相关题目
3.支付宝与“快的打车”联合推出优惠,“快的打车”一夜之间红遍大江南北,据统计,2014年“快的打车”账户流水总金额达到47.3亿元,47.3亿用科学记数法表示为( )
| A. | 4.73×1010 | B. | 47.3×1010 | C. | 4.73×109 | D. | 47.3×109 |
1.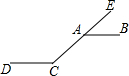 如图,AB∥CD,点E在CA的延长线上.若∠BAE=40°,则∠ACD的大小为( )
如图,AB∥CD,点E在CA的延长线上.若∠BAE=40°,则∠ACD的大小为( )
 如图,AB∥CD,点E在CA的延长线上.若∠BAE=40°,则∠ACD的大小为( )
如图,AB∥CD,点E在CA的延长线上.若∠BAE=40°,则∠ACD的大小为( )| A. | 120° | B. | 130° | C. | 140° | D. | 150° |
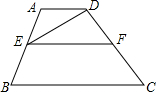 如图,∵∠ADE=∠DEF(已知),
如图,∵∠ADE=∠DEF(已知),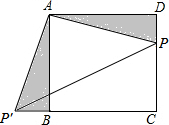 如图,四边形ABCD是正方形,P在CD上,△ADP旋转后能够与△ABP′重合,若AB=3,DP=1,则PP′=2$\sqrt{5}$.
如图,四边形ABCD是正方形,P在CD上,△ADP旋转后能够与△ABP′重合,若AB=3,DP=1,则PP′=2$\sqrt{5}$.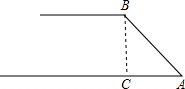 如图,坡长AB=12m,迎水坡AB的坡比为1:$\sqrt{3}$,求堤高BC.
如图,坡长AB=12m,迎水坡AB的坡比为1:$\sqrt{3}$,求堤高BC.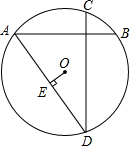 已知AB、CD是⊙O的互相垂直的两条弦,OE⊥AD,垂足为E,求证:OE=$\frac{1}{2}$BC.
已知AB、CD是⊙O的互相垂直的两条弦,OE⊥AD,垂足为E,求证:OE=$\frac{1}{2}$BC.