题目内容
4.若关于x、y的二元一次方程组$\left\{\begin{array}{l}2x+ay=4\\ x+3y=12\end{array}\right.$的解都是正整数,则整数a的值有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 把a看作常数,利用加减消元法求解,根据求出的方程组的解是正整数,可得6-a是20的质因数,然后求解即可.
解答 解:$\left\{\begin{array}{l}{2x+ay=4①}\\{x+3y=12②}\end{array}\right.$,
①-②×2得ay-6y=-20,
解得y=$\frac{20}{6-a}$,
∵20=1×20=2×10=4×5,方程组有正整数解,
∴6-a=1或6-a=20或6-a=2或6-a=10或6-a=4或6-a=5,
∴y=20或1或10或2或5或4,
∴x=-48或9或-18或6或-3或0.
∴整数a的值有2个.
故选:B.
点评 本题考查了解二元一次方程组,把a看作常数,利用代入或加减消元法求解,根据整数解,分子必须是分母的整数倍,要注意对20的正确分解.

练习册系列答案
相关题目
19.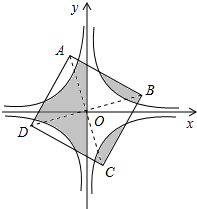 在平面直角坐标系中,有反比例函数y=$\frac{1}{x}$与y=-$\frac{1}{x}$的图象和正方形ABCD,原点O与对角线AC,BD的交点重合,且如图所示的阴影部分面积为8,则AB的长是( )
在平面直角坐标系中,有反比例函数y=$\frac{1}{x}$与y=-$\frac{1}{x}$的图象和正方形ABCD,原点O与对角线AC,BD的交点重合,且如图所示的阴影部分面积为8,则AB的长是( )
 在平面直角坐标系中,有反比例函数y=$\frac{1}{x}$与y=-$\frac{1}{x}$的图象和正方形ABCD,原点O与对角线AC,BD的交点重合,且如图所示的阴影部分面积为8,则AB的长是( )
在平面直角坐标系中,有反比例函数y=$\frac{1}{x}$与y=-$\frac{1}{x}$的图象和正方形ABCD,原点O与对角线AC,BD的交点重合,且如图所示的阴影部分面积为8,则AB的长是( )| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
16.若(am+1bn+2)(a2n-1b2m)=a3b5,则m+n的值为( )
| A. | 1 | B. | 2 | C. | 3 | D. | -3 |
3.已知抛物线y=ax2+2x+c经过点A(0,3),B(1,4)两点,它的解析式为( )
| A. | y=-x2+6x+3 | B. | y=-x2+2x-3 | C. | y=2x2+8x+3 | D. | y=-x2+2x+3 |
 如图在3×4的网格中,每个小正方形的边长都是1个单位长度,定义:以网格中小正方形的顶点为顶点的正方形叫作格点正方形,图中包含“△”的格点正方形的个数有( )
如图在3×4的网格中,每个小正方形的边长都是1个单位长度,定义:以网格中小正方形的顶点为顶点的正方形叫作格点正方形,图中包含“△”的格点正方形的个数有( )
 如图,矩形ABCD的对角线BD经过坐标原点O,矩形ABCD的边分别平行于坐标轴,点C在反比例函数y=$\frac{k}{x}$的图象上.若点A的坐标为(-2,-2),则k的值为( )
如图,矩形ABCD的对角线BD经过坐标原点O,矩形ABCD的边分别平行于坐标轴,点C在反比例函数y=$\frac{k}{x}$的图象上.若点A的坐标为(-2,-2),则k的值为( ) 如图,已知AB∥CD,EF∥MN.
如图,已知AB∥CD,EF∥MN.