题目内容
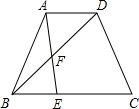 如图,等腰梯形ABCD中,AD∥BC,AD=1,BC=3,AB=CD=2,射线AB绕点A逆时针旋转分别与BD、BC交于点F、E,旋转角∠BAE=∠DBC,则BE=
如图,等腰梯形ABCD中,AD∥BC,AD=1,BC=3,AB=CD=2,射线AB绕点A逆时针旋转分别与BD、BC交于点F、E,旋转角∠BAE=∠DBC,则BE=考点:等腰梯形的性质,旋转的性质
专题:
分析:先由等腰梯形的性质得出△ABE∽△BCD,再列出比例式求解.
解答:解:∵梯形ABCD是等腰梯形,
∴∠ABC=∠C,
又∵∠BAE=∠DBC,
∴△ABE∽△BCD,
∴
=
,
∵BC=3,AB=CD=2,
∴
=
,
∴BE=
.
故答案为:
.
∴∠ABC=∠C,
又∵∠BAE=∠DBC,
∴△ABE∽△BCD,
∴
| AB |
| BC |
| BE |
| DC |
∵BC=3,AB=CD=2,
∴
| 2 |
| 3 |
| BE |
| 2 |
∴BE=
| 4 |
| 3 |
故答案为:
| 4 |
| 3 |
点评:本题主要考查等腰梯形的性质及相似三角形的判定和性质,本题的关键是把知识结合起来,综合运用解题.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案
相关题目
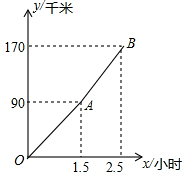 “五一节”期间,王老师一家自驾游去了离家170千米的某地,下面是他们家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象,当他们离目的地还有20千米时,汽车一共行驶的时间是( )
“五一节”期间,王老师一家自驾游去了离家170千米的某地,下面是他们家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象,当他们离目的地还有20千米时,汽车一共行驶的时间是( )| A、2小时 | B、2.2小时 |
| C、2.25小时 | D、2.4小时 |
在平行四边形ABCD中,对角线AC、BD相交于点O,如果AC=10,BD=8,AB=x,则x的取值范围是( )
| A、1<x<9 |
| B、2<x<18 |
| C、8<x<10 |
| D、4<x<5 |
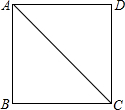 如图,在正方形ABCD中,对角线AC为2,则正方形边长为
如图,在正方形ABCD中,对角线AC为2,则正方形边长为