题目内容
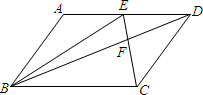 如图,平行四边形ABCD中,E为AD上的任意一点,三角形EFD的面积为4.5平方厘米,三角形BEF的面积为7.5平方厘米,则三角形ABE的面积为
如图,平行四边形ABCD中,E为AD上的任意一点,三角形EFD的面积为4.5平方厘米,三角形BEF的面积为7.5平方厘米,则三角形ABE的面积为考点:平行四边形的性质
专题:
分析:过F作MN⊥AD于点M,交BC于点N,根据△BED和△EFD两个三角形同底,即可求得FM和FN的比值,然后根据△EFD∽△CFB,根据相似三角形的对应边的比等于相似比,即可求得DE和BC的比值,进而求得AE和DE的比值,然后根据三角形的面积公式求解.
解答: 解:过F作MN⊥AD于点M,交BC于点N.
解:过F作MN⊥AD于点M,交BC于点N.
S△BED=S△EFD+S△BEF=4.5+7.5=12(平方厘米),
∵S△EFD=
DE•FM,S△BED=
DE•MN,
∴
=
=
=
.
∴
=
.
∵平行四边形ABCD中AD∥BC,
∴△EFD∽△CFB,
∴
=
=
,
又∵AD=BC,
∴
=
,
∴
=
,
∴S△ABE=
S△BED=
×12=8(平方厘米).
故答案是:8.
 解:过F作MN⊥AD于点M,交BC于点N.
解:过F作MN⊥AD于点M,交BC于点N.S△BED=S△EFD+S△BEF=4.5+7.5=12(平方厘米),
∵S△EFD=
| 1 |
| 2 |
| 1 |
| 2 |
∴
| FM |
| MN |
| S△EFD |
| S△BED |
| 4.5 |
| 12 |
| 3 |
| 8 |
∴
| FM |
| FN |
| 3 |
| 5 |
∵平行四边形ABCD中AD∥BC,
∴△EFD∽△CFB,
∴
| DE |
| BC |
| FM |
| FN |
| 3 |
| 5 |
又∵AD=BC,
∴
| AE |
| DE |
| 2 |
| 3 |
∴
| S△ABE |
| S△BED |
| 2 |
| 3 |
∴S△ABE=
| 2 |
| 3 |
| 2 |
| 3 |
故答案是:8.
点评:本题考查了平行四边形的性质,相似三角形的判定与性质,正确作出辅助线,求得AE与DE的比值是关键.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
 如图,矩形ABCD中对角线交于点O,DE平分∠ADC交BC于E,∠AOB=60°,求∠COE的度数.(提示:说明EC=OC)
如图,矩形ABCD中对角线交于点O,DE平分∠ADC交BC于E,∠AOB=60°,求∠COE的度数.(提示:说明EC=OC)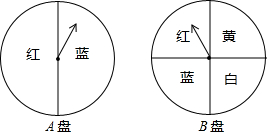 依次转动如图所示的两个转盘进行“配紫色”(红色与蓝色可配得紫色)游戏,每个转盘都被分成面积相等的几个扇形,请你用画树状图或列表的方法,求配得紫色的概率.
依次转动如图所示的两个转盘进行“配紫色”(红色与蓝色可配得紫色)游戏,每个转盘都被分成面积相等的几个扇形,请你用画树状图或列表的方法,求配得紫色的概率.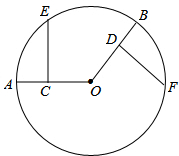 如图,已知AO、BO分别是⊙O的两条半径,C、D分别是AO、BO的中点,CE⊥AO,DF⊥BO.求证:
如图,已知AO、BO分别是⊙O的两条半径,C、D分别是AO、BO的中点,CE⊥AO,DF⊥BO.求证:
 如图是一个正方体盒子的侧面展开图,该正方体六个面上分别标有不同的数字,且相对两个面上的数字是一对相反数.
如图是一个正方体盒子的侧面展开图,该正方体六个面上分别标有不同的数字,且相对两个面上的数字是一对相反数. 如图,在⊙O的弦AB的长等于⊙O的半径,求∠ACB的度数.
如图,在⊙O的弦AB的长等于⊙O的半径,求∠ACB的度数. 如图,∠ABC=∠FAC=90°,BC=3,AB=4,正方形CDEF的周长是52,求AF的长.
如图,∠ABC=∠FAC=90°,BC=3,AB=4,正方形CDEF的周长是52,求AF的长.