题目内容
6.关于x,y的方程组$\left\{\begin{array}{l}{x+2y=3k}\\{2x+y=-2k+1}\end{array}\right.$的解满足x+y>$\frac{3}{5}$.(1)求k的取值范围;
(2)化简|5k+1|-|4-5k|.
分析 (1)方程组两方程相加表示出x+y,代入已知不等式即可求出k的范围;
(2)根据k的范围确定出绝对值里边式子的正负,利用绝对值的代数意义好,去括号合并即可得到结果.
解答 解:(1)$\left\{\begin{array}{l}{x+2y=3k①}\\{2x+y=-2k+1②}\end{array}\right.$,
①+②得:3(x+y)=k+1,即x+y=$\frac{k+1}{3}$,
代入已知不等式得:$\frac{k+1}{3}$>$\frac{3}{5}$,
去分母得:5k+5>9,即k>$\frac{4}{5}$;
(2)∵k>$\frac{4}{5}$,
∴5k+1>0,4-5k<0,
则原式=5k+1+4-5k=5.
点评 此题考查了二元一次方程组的解,以及解一元一次不等式,熟练掌握运算法则是解本题的关键.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
18.下列各式中成立的是( )
| A. | x2y2=(x+y)(x-y) | B. | 1-x2=(1-x)2 | ||
| C. | (x2+4)(-4x)=(x-2)2 | D. | x2-$\frac{1}{4}x+\frac{1}{4}={(x-\frac{1}{2})^2}$ |
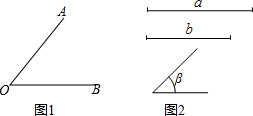 尺规作图(请保留作图痕迹,不写作法).
尺规作图(请保留作图痕迹,不写作法).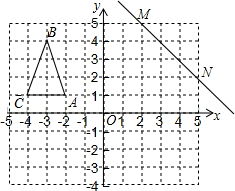 如图,在直角坐标系中有一个格点三角形ABC(顶点都在格点上的三角形),已知A(-2,1),B(-3,4),C(-4,1),直线MN过点M(2,5),N(5,2).
如图,在直角坐标系中有一个格点三角形ABC(顶点都在格点上的三角形),已知A(-2,1),B(-3,4),C(-4,1),直线MN过点M(2,5),N(5,2).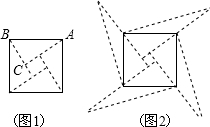 图1是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若AC=6,BC=5,将四个直角三角形中的边长为6的直角边分别向外延长一倍,得到图2所示的“数学风车”,则这个风车的外围周长是( )
图1是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若AC=6,BC=5,将四个直角三角形中的边长为6的直角边分别向外延长一倍,得到图2所示的“数学风车”,则这个风车的外围周长是( ) 如图,已知AB∥CD,∠E=19°,∠D=51°,则∠ABE的度数是70°.
如图,已知AB∥CD,∠E=19°,∠D=51°,则∠ABE的度数是70°.