题目内容
6.阅读材料:求1-2+22-23+…-22015+22016的值.解:设S=1-2+22-23+…-22015+22016,将等式两边同时乘以-2得:
-2S=-2+22-23+…+22016-22017
用上式减去下式得:S-(-2S)=1+22017
即S=$\frac{1}{3}$(22017+1)
故1-2+22-23+…-22015+22016=$\frac{1}{3}$(22017+1).
请你仿照此法计算(请写出计算过程):
(Ⅰ)1-2+22-23+24-25+26;
(Ⅱ)1-2+22-23+…+(-2)n(其中n为自然数).
分析 (Ⅰ)根据题意可以求得题目中所求式子的值;
(Ⅱ)根据题目中的信息,对所求式子变形即可解答本题.
解答 解:(Ⅰ)1-2+22-23+24-25+26
=$\frac{1}{3}×({2}^{7}+1)$
=$\frac{1}{3}×(128+1)$
=$\frac{1}{3}×129$
=43;
(Ⅱ)令S=1-2+22-23+…+(-2)n
则-2S=-2+22-23+…+(-2)n+(-2)n+1,
S-(-2S)=1-(-2)n+1,
解得,S=$\frac{1}{3}[1-(-2)^{n+1}]$,
即1-2+22-23+…+(-2)n=$\frac{1}{3}[1-(-2)^{n+1}]$.
点评 本题考查数字的变化类,解题的关键是明确题意,找出数字的变化特点.

练习册系列答案
相关题目
18.若关于x的方程(k-1)x2-(k-1)x+$\frac{1}{4}$=0有两个相等的实数根,则k的值为( )
| A. | 1 | B. | 2 | C. | 1或2 | D. | 以上都不对 |
16.无论a取何值,下列各式中一定有意义的是( )
| A. | $\sqrt{a+1}$ | B. | $\sqrt{{a^2}-1}$ | C. | a-2 | D. | $\sqrt{{a^2}+1}$ |
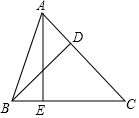 如图,D是△ABC的边AC上一点,CD=2AD,AE⊥BC,交BC于E,若BD=8,tan∠CBD=$\frac{3}{4}$,求AC长.
如图,D是△ABC的边AC上一点,CD=2AD,AE⊥BC,交BC于E,若BD=8,tan∠CBD=$\frac{3}{4}$,求AC长. 已知△ABC与△BDE都是正三角形,点A、B、E在同一直线上,求证:AD=CE.
已知△ABC与△BDE都是正三角形,点A、B、E在同一直线上,求证:AD=CE. 如图,在数轴上有A,B两点(点A在点B的右边),点A表示a,点B表示-2a+3,且点A,B之间的距离是6,则a=3.
如图,在数轴上有A,B两点(点A在点B的右边),点A表示a,点B表示-2a+3,且点A,B之间的距离是6,则a=3.